题目内容
10. 如图,已知AB=CD,AB∥CD,BE=CF,求证:AF∥ED.
如图,已知AB=CD,AB∥CD,BE=CF,求证:AF∥ED.
分析 根据两直线平行,内错角相等可得∠B=∠C,再求出BF=CE,然后利用“边角边”证明△ABF和△DCE全等,根据全等三角形对应角相等可得∠AFB=∠DEC,最后利用内错角相等,两直线平行证明即可.
解答 证明:∵AB∥CD,
∴∠B=∠C,
∵BE=CF,
∴BE+EF=CF+EF,
即BF=CE,
在△ABF和△DCE中,$\left\{\begin{array}{l}{AB=CD}\\{∠B=∠C}\\{BF=CE}\end{array}\right.$,
∴△ABF≌△DCE(SAS),
∴∠AFB=∠DEC,
∴AF=ED.
点评 本题考查了全等三角形的判定与性质,平行线的性质与判定,熟练掌握三角形全等的判定方法并准确识图是解题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
20.下列大小比较正确的是( )
| A. | $\sqrt{2}$>$\sqrt{3}$ | B. | 2<$\sqrt{5}$ | C. | 2$\sqrt{2}$<$\sqrt{5}$ | D. | 0<-$\sqrt{2}$ |
5.4的算术平方根是( )
| A. | ±4 | B. | 4 | C. | ±2 | D. | 2 |
2.某地某天的最低气温为-5℃,最高气温为13℃,那么这一天的最高气温比最低气温高( )
| A. | 18℃ | B. | 13℃ | C. | 8℃ | D. | 5℃ |
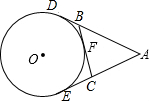 如图,AE,AD,BC分别切⊙O于点E、D和点F,若AD=8cm,则△ABC的周长为16cm.
如图,AE,AD,BC分别切⊙O于点E、D和点F,若AD=8cm,则△ABC的周长为16cm. 在平面直角坐标系中,$A(6\sqrt{3},0),B(0,6)$,动点M从点O开始沿OA以$\sqrt{3}$cm/s的速度向点A移动,动点N从点A开始沿AB以2cm/s的速度向点B移动.如果M,N分别从O,A同时移动,移动时间为t(0<t<6).
在平面直角坐标系中,$A(6\sqrt{3},0),B(0,6)$,动点M从点O开始沿OA以$\sqrt{3}$cm/s的速度向点A移动,动点N从点A开始沿AB以2cm/s的速度向点B移动.如果M,N分别从O,A同时移动,移动时间为t(0<t<6).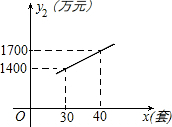 某企业生成一种节能产品,投放市场供不应求.若该企业每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于120万元.已知这种产品的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=190-2x.月产量x(套)与生成总成本y2(万元)存在如图所示的函数关系.
某企业生成一种节能产品,投放市场供不应求.若该企业每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于120万元.已知这种产品的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=190-2x.月产量x(套)与生成总成本y2(万元)存在如图所示的函数关系.