题目内容
15.如图①,在△ABC中,AB=AC,点D,E分别在边BC、AC上,连接DE,且DE=DC.(1)问题发现:若∠ABC=∠EDC=90°,则$\frac{AE}{BD}$=$\sqrt{2}$;
(2)拓展探究,若∠ABC=∠EDC=120°,将△EDC绕点C按顺时针方向旋转到如图②所示的位置,则$\frac{AE}{BD}$的大小有无变化?若不变,请加以证明;若变化,请求出$\frac{AE}{BD}$的值.
(3)问题解决:当△EDC旋转到如图③所示的位置时,若∠ABC=∠EDC=2α(0°<α<90°),则$\frac{AE}{BD}$的值为2sinα(用含a的式子表示)

分析 (1)如图1中,作EF⊥AB于F.首先证明四边形BDEF是矩形,再证明在Rt△AEF中,根据tan∠A=$\frac{EF}{AE}$=$\frac{\sqrt{2}}{2}$即可解决问题.
(2)由△ABC∽△EDC,推出$\frac{BC}{DC}$=$\frac{AC}{CE}$,即$\frac{BC}{AC}$=$\frac{DC}{EC}$,推出△ACE∽△BCD,推出$\frac{AE}{BD}$=$\frac{EC}{DC}$,在△EDC中,过点D作DH⊥EC于点H,则EC=2CH,在Rt△CDH中,CH=CD•sin60°=$\frac{\sqrt{3}}{2}$CD,推出EC=$\sqrt{3}$CD,即可解决问题.
(3)只要证明$\frac{AE}{BD}$=$\frac{EC}{DC}$=2sinα,即可,方法类似(2).
解答 解:(1)如图1中,作EF⊥AB于F.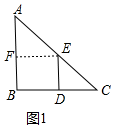
∵∠FBD=∠BDE=∠EFB=90°,
∴四边形BDEF是矩形,
∴EF=BD,
在Rt△AEF中,∵∠AFE=90°,∠A=45°,
∴tan∠A=$\frac{EF}{AE}$=$\frac{\sqrt{2}}{2}$,
∴AE=$\sqrt{2}$EF,
∴$\frac{AE}{BD}$=$\sqrt{2}$,
故答案为$\sqrt{2}$
(2)如图2中,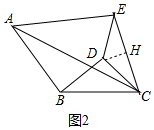
由题意知,△ABC和△EDC都是等腰三角形,且∠ABC=∠EDC=120°,
∴∠ACB=∠CAB=∠ECD=∠CED=30°,
∴△ABC∽△EDC,
∴$\frac{BC}{DC}$=$\frac{AC}{CE}$,即$\frac{BC}{AC}$=$\frac{DC}{EC}$,
又∠ECD+∠DCA=∠ACB+∠DCA,
∴∠DCB=∠ECA,
∴△ACE∽△BCD,
∴$\frac{AE}{BD}$=$\frac{EC}{DC}$,
在△EDC中,过点D作DH⊥EC于点H,则EC=2CH,
在Rt△CDH中,CH=CD•sin60°=$\frac{\sqrt{3}}{2}$CD,
∴EC=$\sqrt{3}$CD.
∴$\frac{AE}{BD}$=$\frac{EC}{DC}$=$\sqrt{3}$.
(3)如图3中,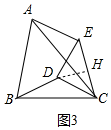
由题意知,△ABC和△EDC都是等腰三角形,且∠ABC=∠EDC=2α,
∴∠ACB=∠CAB=∠ECD=∠CED=90°-α,
∴△ABC∽△EDC,
∴$\frac{BC}{DC}$=$\frac{AC}{CE}$,即$\frac{BC}{AC}$=$\frac{DC}{EC}$,
又∠ECD+∠DCA=∠ACB+∠DCA,
∴∠DCB=∠ECA,
∴△ACE∽△BCD,
∴$\frac{AE}{BD}$=$\frac{EC}{DC}$,
在△EDC中,过点D作DH⊥EC于点H,则EC=2CH,∠CDH=∠HDE=α,
在Rt△CDH中,CH=CD•sinα,
∴EC=2CD•sinα.
∴$\frac{AE}{BD}$=$\frac{EC}{DC}$=2sinα,
故答案为2sinα
点评 本题课程是三角形综合题、等腰直角三角形的性质、等腰三角形的性质、锐角三角函数、相似三角形的判定和性质等知识,解题的关键是灵活运用相似三角形的判定和性质解决问题,属于中考常考题型.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | ±4 | B. | 4 | C. | ±2 | D. | 2 |
| A. | F+V-E=2 | B. | F+E-V=2 | C. | E+V-F=2 | D. | E-V-F=2 |
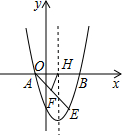 如图,抛物线y=x2+bx+c经过点A(-1,0),B(3,0).
如图,抛物线y=x2+bx+c经过点A(-1,0),B(3,0).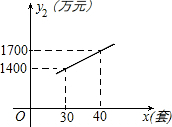 某企业生成一种节能产品,投放市场供不应求.若该企业每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于120万元.已知这种产品的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=190-2x.月产量x(套)与生成总成本y2(万元)存在如图所示的函数关系.
某企业生成一种节能产品,投放市场供不应求.若该企业每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于120万元.已知这种产品的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=190-2x.月产量x(套)与生成总成本y2(万元)存在如图所示的函数关系.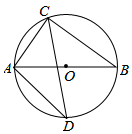 如图,AB是⊙O的直径,弦AC=6,BC=8,弦CD平分∠ACB.
如图,AB是⊙O的直径,弦AC=6,BC=8,弦CD平分∠ACB.