题目内容
8．不等式组$\left\{\begin{array}{l}{x+1＞0}\\{x+2≥4x-1}\end{array}\right.$的解集为-1＜x≤1．分析 先求出其中各不等式的解集，再求出这些解集的公共部分即可．
解答 解：$\left\{\begin{array}{l}{x+1＞0}&{①}\\{x+2≥4x-1}&{②}\end{array}\right.$，
由①得x＞-1，
由②得x≤1，
∴不等式组的就为-1＜x≤1．
故答案为-1＜x≤1．
点评 本题考查一元一次不等式组，一元一次不等式等知识，理解不等式组解的定义是解题的关键，可以利用数轴寻找解的公共部分，属于中考常考题型．
练习册系列答案
习题精选系列答案
相关题目
19．在$\frac{{x}^{2}-3}{5}$，-xy2，$\frac{1}{2π}$，$\frac{a}{3}$，ax2+bx+c，a3b3，$\frac{ab}{2}$中，单项式有（ ）
| A． | 2个 | B． | 3个 | C． | 4个 | D． | 5个 |
16．
正方形ABCD的边长为1，其面积记为S1，以CD为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积记为S2，…按此规律继续下去，则S9的值为（ ）
正方形ABCD的边长为1，其面积记为S1，以CD为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积记为S2，…按此规律继续下去，则S9的值为（ ）| A． | ${（{\frac{1}{2}}）^9}$ | B． | ${（{\frac{1}{2}}）^8}$ | C． | ${（{\frac{{\sqrt{2}}}{2}}）^9}$ | D． | ${（{\frac{{\sqrt{2}}}{2}}）^8}$ |
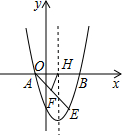如图，抛物线y=x2+bx+c经过点A（-1，0），B（3，0）．
有一直经为$\sqrt{2}$cm圆形纸片，从中剪出一个圆心角是90°的最大扇形ABC（如图所示）．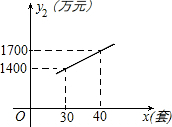
某企业生成一种节能产品，投放市场供不应求．若该企业每月的产量保持在一定的范围，每套产品的生产成本不高于50万元，每套产品的售价不低于120万元．已知这种产品的月产量x（套）与每套的售价y1（万元）之间满足关系式y1=190-2x．月产量x（套）与生成总成本y2（万元）存在如图所示的函数关系．