题目内容
5.如图1,△ABC是等腰直角三角形,∠BAC=90°,AB=AC,四边形ADEF是正方形,点B.C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.
(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明,若不成立,请说明理由.
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长BD交CF于点H.
①探究BD与CF之间的位置关系,并说明理由;
②当AB=$\sqrt{2}$,AD=$\sqrt{3}+1$时,求线段DH的长.
分析 (1)结论:BD=CF.只要证明△ABD≌△ACF即可.
(2)①在利用“8字型”证明∠FHN=∠DAN=90°,即可解决问题.
②如图4中,连接DF,延长AB,与DF交于点M.在Rt△ADM中,求出BM、DM,再利用勾股定理即可解决问题.
解答 (l)解:如图2中,BD=CF成立.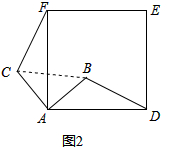
理由:由旋转得:AC=AB,∠CAF=∠BAD=θ;AF=AD,
在△ABD和△ACF中,$\left\{\begin{array}{l}{AD=AF}\\{∠BAD=∠CAF}\\{AB=CA}\end{array}\right.$,
∴△ABD≌△ACF,
∴BD=CF.
(2)①证明:如图3中,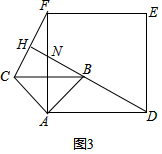
由(1)得,△ABD≌△ACF,
∴∠HFN=∠ADN,
∵∠HNF=∠AND,∠AND+∠AND=90°
∴∠HFN+∠HNF=90°
∴∠NHF=90°,
∴HD⊥HF,即BD⊥CF.
②如图4中,连接DF,延长AB,与DF交于点M.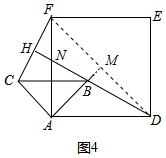
∵四边形ADEF是正方形,
∴∠MDA=45°,
∵∠MAD=45°
∴∠MAD=∠MDA,∠AMD=90°,
∴AM=DM,
∵AD=$\sqrt{3}$+1,
在△MAD中,AM2+DM2=AD2,
∴AM=DM=$\frac{\sqrt{6}+\sqrt{2}}{2}$,
∴MB=AM-AB=$\frac{\sqrt{6}+\sqrt{2}}{2}$-$\sqrt{2}$=$\frac{\sqrt{6}-\sqrt{2}}{2}$,
在Rt△BMD中,BM2+DM2=BD2,
∴BD=$\sqrt{B{M}^{2}+D{M}^{2}}$=2.
在Rt△ADF中,AD=$\sqrt{3}$+1,
∴DF=$\sqrt{2}$AD=$\sqrt{6}$+$\sqrt{2}$,
由②知,HD⊥HF,
∴∠DHF=∠DMB=90°,
∵∠BDM=∠FDH,
∴△BDM∽△FDH,
∴$\frac{BD}{DF}=\frac{DM}{DH}$,
∴DH=$\frac{DF•DM}{BD}$=$\frac{(\sqrt{6}+\sqrt{2})×\frac{\sqrt{6}+\sqrt{2}}{2}}{2}$=2+$\sqrt{3}$.
点评 此题考查四边形综合题、正方形的性质、等腰直角三角形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是正确寻找全等三角形解决问题,属于中考压轴题.

 名校课堂系列答案
名校课堂系列答案 正方形ABCD的边长为1,其面积记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为S2,…按此规律继续下去,则S9的值为( )
正方形ABCD的边长为1,其面积记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为S2,…按此规律继续下去,则S9的值为( )| A. | ${({\frac{1}{2}})^9}$ | B. | ${({\frac{1}{2}})^8}$ | C. | ${({\frac{{\sqrt{2}}}{2}})^9}$ | D. | ${({\frac{{\sqrt{2}}}{2}})^8}$ |
 如图,AB为⊙O的直径,AB=4$\sqrt{3}$,点C为半圆AB上一动点,以BC为边向⊙O外作正△BCD(点D在直线AB的上方),连接OD,则线段OD的长( )
如图,AB为⊙O的直径,AB=4$\sqrt{3}$,点C为半圆AB上一动点,以BC为边向⊙O外作正△BCD(点D在直线AB的上方),连接OD,则线段OD的长( )| A. | 随点C的运动而变化,最大值为4 | B. | 随点C的运动而变化,最大值为4$\sqrt{3}$ | ||
| C. | 随点C的运动而变化,最小值为2 | D. | 随点C的运动而变化,但无最值 |
 在平面直角坐标系中,$A(6\sqrt{3},0),B(0,6)$,动点M从点O开始沿OA以$\sqrt{3}$cm/s的速度向点A移动,动点N从点A开始沿AB以2cm/s的速度向点B移动.如果M,N分别从O,A同时移动,移动时间为t(0<t<6).
在平面直角坐标系中,$A(6\sqrt{3},0),B(0,6)$,动点M从点O开始沿OA以$\sqrt{3}$cm/s的速度向点A移动,动点N从点A开始沿AB以2cm/s的速度向点B移动.如果M,N分别从O,A同时移动,移动时间为t(0<t<6). 有一直经为$\sqrt{2}$cm圆形纸片,从中剪出一个圆心角是90°的最大扇形ABC(如图所示).
有一直经为$\sqrt{2}$cm圆形纸片,从中剪出一个圆心角是90°的最大扇形ABC(如图所示).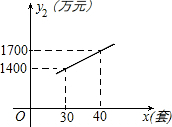 某企业生成一种节能产品,投放市场供不应求.若该企业每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于120万元.已知这种产品的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=190-2x.月产量x(套)与生成总成本y2(万元)存在如图所示的函数关系.
某企业生成一种节能产品,投放市场供不应求.若该企业每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于120万元.已知这种产品的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=190-2x.月产量x(套)与生成总成本y2(万元)存在如图所示的函数关系. 如图,正方形ABCD的边长为2,以BC为边向正方形内作等边△BCE,连接AE、DE.
如图,正方形ABCD的边长为2,以BC为边向正方形内作等边△BCE,连接AE、DE. 如图,作出△ABC的三条高.
如图,作出△ABC的三条高.