题目内容
18.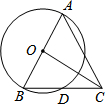 如图,AB是⊙O的直径,BD是⊙O的弦,延长BD至点C,使得DC=BD,连接AC,OC.若AB=5,BD=$\sqrt{5}$,则OC的长为( )
如图,AB是⊙O的直径,BD是⊙O的弦,延长BD至点C,使得DC=BD,连接AC,OC.若AB=5,BD=$\sqrt{5}$,则OC的长为( )| A. | 4 | B. | $\frac{5}{2}$$\sqrt{3}$ | C. | $\frac{9}{5}$$\sqrt{5}$ | D. | $\frac{\sqrt{65}}{2}$ |
分析 连接AD,作OH⊥BC于H.利用勾股定理求出AD,利用三角形中位线定理求出OH,在Rt△OHC中,根据OC=$\sqrt{O{H}^{2}+C{H}^{2}}$即可解决问题.
解答 解:连接AD,作OH⊥BC于H.
∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC.
∴在直角△ABD中,AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{25-5}$=2$\sqrt{5}$,
∵OH⊥BC,AD⊥BC,
∴OH∥AD,∵OB=OA,
∴BH=HD=$\frac{\sqrt{5}}{2}$,OH=$\frac{1}{2}$AD=$\sqrt{5}$,CH=$\frac{3}{2}$$\sqrt{5}$,
在Rt△OCH中,OC=$\sqrt{O{H}^{2}+C{H}^{2}}$=$\frac{\sqrt{65}}{2}$.
故选D.
点评 本题考查圆的有关知识、勾股定理、三角形的中位线定理等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
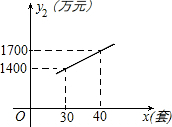 某企业生成一种节能产品,投放市场供不应求.若该企业每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于120万元.已知这种产品的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=190-2x.月产量x(套)与生成总成本y2(万元)存在如图所示的函数关系.
某企业生成一种节能产品,投放市场供不应求.若该企业每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于120万元.已知这种产品的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=190-2x.月产量x(套)与生成总成本y2(万元)存在如图所示的函数关系.
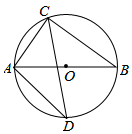 如图,AB是⊙O的直径,弦AC=6,BC=8,弦CD平分∠ACB.
如图,AB是⊙O的直径,弦AC=6,BC=8,弦CD平分∠ACB. 如图,作出△ABC的三条高.
如图,作出△ABC的三条高. a,b,c大小关系如图,下列各式①b+a+(-c)>0;②(-a)-b+c>0;③$\frac{a}{|a|}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=1;④bc-a>0;⑤|a-b|-|c+b|+|a-c|=-2b,其中正确的有( )
a,b,c大小关系如图,下列各式①b+a+(-c)>0;②(-a)-b+c>0;③$\frac{a}{|a|}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$=1;④bc-a>0;⑤|a-b|-|c+b|+|a-c|=-2b,其中正确的有( )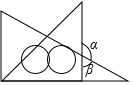 如果我们将一副三角尺按如图所示的位置摆放,并且已知∠a=118°28',那么∠B的度数为61°32'.
如果我们将一副三角尺按如图所示的位置摆放,并且已知∠a=118°28',那么∠B的度数为61°32'. 如图,△ABC中,∠CAB的平分线与BC的垂直平分线相交于D,过点D作DE⊥AB,DF⊥AC,求证:BE=CF.
如图,△ABC中,∠CAB的平分线与BC的垂直平分线相交于D,过点D作DE⊥AB,DF⊥AC,求证:BE=CF.