题目内容
12.已知关于x的方程(x-2)2-4|x-2|-k=0有四个根,则k的范围为( )| A. | -1<k<0 | B. | -4<k<0 | C. | 0<k<1 | D. | 0<k<4 |
分析 根据已知条件得到|x-2|2-4|x-2|-k=0有两个不同根,推出△=16+4k>0,即k>-4,且两根的积为正数,即-k>0,即刻得到结论.
解答 解:∵关于x的方程(x-2)2-4|x-2|-k=0有四个根,
>2-4|x-2|-k=0有两个不同根,
∴△=16+4k>0,即k>-4,
且两根的积为正数,即-k>0,
∴k<0,
∴k的范围为-4<k<0;
故选B.
点评 本题考查了根的判别式,一元二次方程根的情况与判别式△的关系:(1)△>0?方程有两个不相等的实数根;(2)△=0?方程有两个相等的实数根;(3)△<0?方程没有实数根.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
7.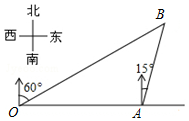 如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
 如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )
如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )| A. | 3$\sqrt{2}$km | B. | 3$\sqrt{3}$km | C. | 4 km | D. | (3$\sqrt{3}$-3)km |
17.如图是一副眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称.AB∥x轴,AB=4cm,最低点C在x轴上,高CH=1cm,BD=2cm,则右轮廓线DFE所在抛物线的函数解析式为( )
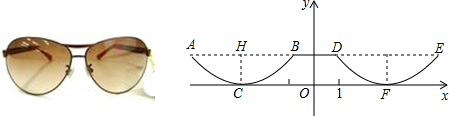

| A. | $y=\frac{1}{4}{(x+3)^2}$ | B. | $y=-\frac{1}{4}{(x+3)^2}$ | C. | $y=-\frac{1}{4}{(x-3)^2}$ | D. | $y=\frac{1}{4}{(x-3)^2}$ |
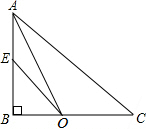 在△ABC中,∠ABC=90°,∠BAC的平分线AO交BC于O点,E为边AB上一点,且OE=OC,若AC=10,AB=6,求AE的长.
在△ABC中,∠ABC=90°,∠BAC的平分线AO交BC于O点,E为边AB上一点,且OE=OC,若AC=10,AB=6,求AE的长.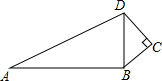 如图,已知∠C=90°,AB=12,BC=3,CD=4,∠ABD=90°,则AD=13.
如图,已知∠C=90°,AB=12,BC=3,CD=4,∠ABD=90°,则AD=13.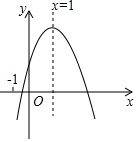 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列五个结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列五个结论: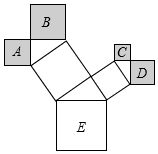 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别是3、5、2、3,则最大正方形E的面积是( )
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别是3、5、2、3,则最大正方形E的面积是( )