题目内容
1.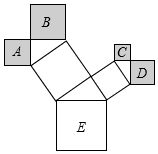 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别是3、5、2、3,则最大正方形E的面积是( )
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别是3、5、2、3,则最大正方形E的面积是( )| A. | 8 | B. | 10 | C. | 13 | D. | 15 |
分析 分别设中间两个正方形和最大正方形的边长为x,y,z,由勾股定理得出x2=8,y2=5,z2=x2+y2,即最大正方形的面积为z2.
解答 解:设中间两个正方形的边长分别为x、y,最大正方形E的边长为z,则由勾股定理得:
x2=3+5=8,y2=2+3=5,z2=x2+y2=13;
即最大正方形E的面积为:z2=13.
故选:C.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
12.已知关于x的方程(x-2)2-4|x-2|-k=0有四个根,则k的范围为( )
| A. | -1<k<0 | B. | -4<k<0 | C. | 0<k<1 | D. | 0<k<4 |
9.化简或求值:
(1)化简:(4ab-b2)-2(a2+2ab-b2)
(2)先化简,再求值:2(3b2-a3b)-3(2b2-a2b-a3b)-4a2b,其中a=-$\frac{1}{2}$,b=8.
(1)化简:(4ab-b2)-2(a2+2ab-b2)
(2)先化简,再求值:2(3b2-a3b)-3(2b2-a2b-a3b)-4a2b,其中a=-$\frac{1}{2}$,b=8.
10.下列图形中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
11.若抛物线y=(x-m)2+(m+1)的顶点在第一象限,则m的取值范围为( )
| A. | m>2 | B. | m>0 | C. | m>-1 | D. | -1<m<0 |
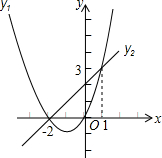 如图是二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象,观察图象写出y2<y1时,x的取值范围x>1或x<-2.
如图是二次函数y1=ax2+bx+c和一次函数y2=mx+n的图象,观察图象写出y2<y1时,x的取值范围x>1或x<-2.