题目内容
13.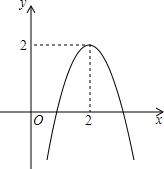 已知二次函数y=ax2+bx+c的图象如图所示,则a<0,b>0,4ac-b2<0(填“<”或“>”)a+b+c=0,4a+2b+c=2,对称轴方程直线x=2;函数解析式y=-2x2+8x-6;当x>2时,y随x的增大而减小;由图象回答;当y>0时,x的取值范围1<x<2;当y=0时,x=1或3;当y<0时,x的取值范围x<1或x>3.
已知二次函数y=ax2+bx+c的图象如图所示,则a<0,b>0,4ac-b2<0(填“<”或“>”)a+b+c=0,4a+2b+c=2,对称轴方程直线x=2;函数解析式y=-2x2+8x-6;当x>2时,y随x的增大而减小;由图象回答;当y>0时,x的取值范围1<x<2;当y=0时,x=1或3;当y<0时,x的取值范围x<1或x>3.
分析 根据抛物线的开口方向判断a的符号,根据左同右异的原则判断b的符号,根据图象得出抛物线和x轴的交点坐标,当x=1时,y=0,对称轴方程为x=2,根据图象得出y随x的增大而减小以及y>0,y<0和y=0时x的取值范围即可.;
解答 解:∵抛物线的开口向下,
∴a<0,
∵对称轴在y轴右侧,
∴b>0,
∵抛物线与x轴的交点有两个,
∴b2-4ac>0,
∴4ac-b2<0,
根据图象得出抛物线和x轴的交点坐标(1,0)(3,0),
∴当x=1时,y=0,即a+b+c=0,
∴对称轴方程为x=2,
设抛物线的解析式为ya(x-h)2+k,
点坐标(2,2),
∴函数解析式y=-2x2+8x-6;
根据图象得,当x>2时,y随x的增大而减小,
当y>0时,1<x<2,
当y<0时,x<1或x>3,
当y=0时x=1或3.
故答案为<,>,<,0;2,直线x=2,y=-2x2+8x-6;>2,1<x<2,1或3,x<1或x>3.
点评 本题考查了二次函数图象与系数的关系,二次函数的性质,确定抛物线的开口方向、对称轴、顶点的坐标,以及与x、y轴的交点坐标是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,直线a∥b∥c,若$\frac{AC}{CE}$=$\frac{2}{3}$,BD=3,则DF的长为4.5.
如图,直线a∥b∥c,若$\frac{AC}{CE}$=$\frac{2}{3}$,BD=3,则DF的长为4.5. 如图,AB⊥BD,EF⊥BD,CD⊥BD,且AB:EF:CD=3:5:8 求AE:EC的值.
如图,AB⊥BD,EF⊥BD,CD⊥BD,且AB:EF:CD=3:5:8 求AE:EC的值. 如图,△ABC中∠B的外角平分线BD于∠C的外角平分线CE相交于点P,求证:点P在∠ABC的角平分线上.
如图,△ABC中∠B的外角平分线BD于∠C的外角平分线CE相交于点P,求证:点P在∠ABC的角平分线上.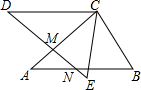 如图,AB=DE,AC=DC,BC=EC,DE与AC、AB分别交于点M、N,CE与AB交于点H,且∠A=∠BCE=40°,∠B=60°
如图,AB=DE,AC=DC,BC=EC,DE与AC、AB分别交于点M、N,CE与AB交于点H,且∠A=∠BCE=40°,∠B=60°