题目内容
17.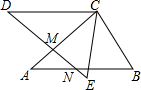 如图,AB=DE,AC=DC,BC=EC,DE与AC、AB分别交于点M、N,CE与AB交于点H,且∠A=∠BCE=40°,∠B=60°
如图,AB=DE,AC=DC,BC=EC,DE与AC、AB分别交于点M、N,CE与AB交于点H,且∠A=∠BCE=40°,∠B=60°(1)求证:△ABC≌△DEC;
(2)求证:AB∥CD;
(3)图中与∠ACB相等的角一共有5个.
分析 (1)利用SSS证明△ABC≌△DEC即可;
(2)利用全等三角形的性质得出∠ACB=∠DCE,进而利用平行线的判定证明即可;
(3)利用全等三角形的性质和角的关系解答即可.
解答 证明:(1)在△ABC与△DEC中,
$\left\{\begin{array}{l}{AB=DE}\\{AC=DC}\\{BC=EC}\end{array}\right.$,
∴△ABC≌△DEC(SSS);
(2)∵△ABC≌△DEC,
∴∠ACB=∠DCE,
∴∠DCA=∠BCE=40°,
∵∠A=∠BCE=40°,
∴∠A=∠DCA=40°,
∴AB∥CD;
(3)与∠ACB相等的角是∠DCE等共5个.
故答案为:5
点评 本题考查了全等三角形的性质和判定的应用,注意:全等三角形的对应边相等,全等三角形的判定定理有SAS,ASA,AAS,SSS.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.如图是由4个大小相同的正方体搭成的几何体,小彬又拿来2个同样的正方体加上去,得到的新几何体的主视图和左视图如图所示,则添加的正方体不可能摆放在( )


| A. | 1号的前后 | B. | 2号的前后 | C. | 3号的前后 | D. | 4号的左右 |
6.若抛物线y=x2+(m2+m-6)x+(m+3)的顶点在y轴的正半轴上,则m的取值是( )
| A. | 2 | B. | -2 | C. | 3 | D. | -3 |
7.已知代数式x-2y的值是5,则代数式3x-6y+1的值是( )
| A. | 16 | B. | -14 | C. | 14 | D. | -16 |
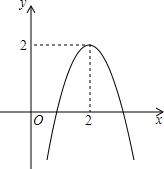 已知二次函数y=ax2+bx+c的图象如图所示,则a<0,b>0,4ac-b2<0(填“<”或“>”)a+b+c=0,4a+2b+c=2,对称轴方程直线x=2;函数解析式y=-2x2+8x-6;当x>2时,y随x的增大而减小;由图象回答;当y>0时,x的取值范围1<x<2;当y=0时,x=1或3;当y<0时,x的取值范围x<1或x>3.
已知二次函数y=ax2+bx+c的图象如图所示,则a<0,b>0,4ac-b2<0(填“<”或“>”)a+b+c=0,4a+2b+c=2,对称轴方程直线x=2;函数解析式y=-2x2+8x-6;当x>2时,y随x的增大而减小;由图象回答;当y>0时,x的取值范围1<x<2;当y=0时,x=1或3;当y<0时,x的取值范围x<1或x>3.