题目内容
5．已知$\frac{x}{3}$=$\frac{y}{5}$=$\frac{z}{7}$≠0，求下列各式的值：（1）$\frac{x+y+z}{y}$；
（2）$\frac{2x+3y+4z}{5x-3y+z}$．
分析 （1）根据比例的性质，可用x表示y，用x表示z，根据分式的性质，可得答案；
（2）根据比例的性质，可用x表示y，用x表示z，根据分式的性质，可得答案．
解答 解：（1）由$\frac{x}{3}$=$\frac{y}{5}$=$\frac{z}{7}$≠0，得
y=$\frac{5x}{3}$，z=$\frac{7x}{3}$．
$\frac{x+y+z}{y}$=$\frac{x+\frac{5}{3}x+\frac{7}{3}x}{\frac{5}{3}x}$=$\frac{5x}{\frac{5}{3}x}$=3；
（2）$\frac{2x+3y+4z}{5x-3y+z}$=$\frac{2x+3×\frac{5x}{3}+4×\frac{7x}{3}}{5x-3×\frac{5x}{3}+\frac{7x}{3}}$=$\frac{\frac{49}{3}x}{\frac{7x}{3}}$=7．
点评 本题考查了比例的性质，利用比的性质得出y=$\frac{5x}{3}$，z=$\frac{7x}{3}$是解题关键．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
在图中共有多少条射线？把能表示出来的射线表示出来．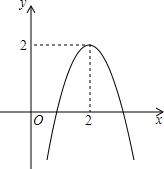
已知二次函数y=ax2+bx+c的图象如图所示，则a＜0，b＞0，4ac-b2＜0（填“＜”或“＞”）a+b+c=0，4a+2b+c=2，对称轴方程直线x=2；函数解析式y=-2x2+8x-6；当x＞2时，y随x的增大而减小；由图象回答；当y＞0时，x的取值范围1＜x＜2；当y=0时，x=1或3；当y＜0时，x的取值范围x＜1或x＞3．
9．如图是由4个大小相同的正方体搭成的几何体，小彬又拿来2个同样的正方体加上去，得到的新几何体的主视图和左视图如图所示，则添加的正方体不可能摆放在（ ）
| A． | 1号的前后 | B． | 2号的前后 | C． | 3号的前后 | D． | 4号的左右 |
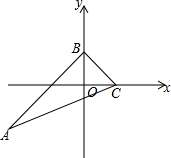如图，△ABC的三条内角平分线交点在y轴上，点C的坐标为（2，0），点B的坐标为（0，2），直线AC的解析式为y=$\frac{1}{2}$x-1，则tanA的值是$\frac{1}{3}$．