题目内容
5.若-4≤x≤3,化简$\sqrt{{x}^{2}+8x+16}$-$\sqrt{{x}^{2}-6x+9}$的结果为( )| A. | 2x+1 | B. | -2x-1 | C. | 1 | D. | 7 |
分析 原式被开方数利用完全平方公式化简,根据x的范围判断出x+4与x-3的正负,利用二次根式性质及绝对值的代数意义化简,去括号合并即可得到结果.
解答 解:∵-4≤x≤3,
∴x+4≥0,x-3≤0,
则原式=$\sqrt{(x+4)^{2}}$-$\sqrt{(x-3)^{2}}$=|x+4|-|x-3|=x+4+x-3=2x+1,
故选A
点评 此题考查了二次根式的性质与化简,绝对值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15.观察下列4个命题:其中真命题是( )
(1)三角形的外角和是180°;
(2)三角形的三个内角中至少有两个锐角;
(3)直角三角形两锐角互余;
(4)相等的角是对顶角.
(1)三角形的外角和是180°;
(2)三角形的三个内角中至少有两个锐角;
(3)直角三角形两锐角互余;
(4)相等的角是对顶角.
| A. | (1)(2) | B. | (2)(3) | C. | (2)(4) | D. | (3)(4) |
16.计算结果为x2+7x-18的是( )
| A. | (x+2)(x-9) | B. | (x-2)(x+9) | C. | (x+3)(x+9) | D. | (x-3)(x+6) |
13.若2m=3,2n=4,则23m-2n等于( )
| A. | $\frac{27}{16}$ | B. | $\frac{27}{8}$ | C. | $\frac{9}{8}$ | D. | 11 |
10.在函数y=$\frac{\sqrt{3x+6}}{x}$中,自变量x的取值范围是( )
| A. | x≥-2 | B. | x>-0 | C. | x≥-2且x≠0 | D. | x>-2且x≠0 |
17.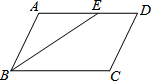 如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=4,DE=2,则平行四边形ABCD的面积最大为( )
如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=4,DE=2,则平行四边形ABCD的面积最大为( )
 如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=4,DE=2,则平行四边形ABCD的面积最大为( )
如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=4,DE=2,则平行四边形ABCD的面积最大为( )| A. | 12 | B. | 18 | C. | 24 | D. | 32 |
14.函数y=kx-1(常数k>0)的图象不经过的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.等腰三角形腰长为5,则其底边长a的取值范围为( )
| A. | 0<a≤5 | B. | 5≤a≤10 | C. | 0<a<10 | D. | 0<a<5 |
