题目内容
7.在Rt△ABC中,∠C=90°,BC=12,AC=16,则斜边AB边上的高CD的长是( )| A. | 20 | B. | 10 | C. | 9.6 | D. | 8 |
分析 根据勾股定理求得AB的长;根据直角三角形的面积公式求得CD的长.
解答  解:如图,
解:如图,
∵在Rt△ABC中,∠ACB=90°,AC=16,BC=12,
∴根据勾股定理,得AB=20.
又∵CD⊥AB,
∴CD=$\frac{AC•BC}{AB}$=9.6.
故CD的长是9.6.
故选:C.
点评 此题综合考查了勾股定理和直角三角形的面积公式.直角三角形斜边上的高等于两条直角边的乘积除以斜边.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
17.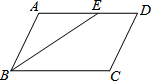 如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=4,DE=2,则平行四边形ABCD的面积最大为( )
如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=4,DE=2,则平行四边形ABCD的面积最大为( )
 如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=4,DE=2,则平行四边形ABCD的面积最大为( )
如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=4,DE=2,则平行四边形ABCD的面积最大为( )| A. | 12 | B. | 18 | C. | 24 | D. | 32 |
18. 如图,将△ABC绕点C按顺时针方向旋转至△A′B′C′,使点A′落在BC的延长线上,已知∠A=30°,∠B=40°,则旋转角为( )
如图,将△ABC绕点C按顺时针方向旋转至△A′B′C′,使点A′落在BC的延长线上,已知∠A=30°,∠B=40°,则旋转角为( )
 如图,将△ABC绕点C按顺时针方向旋转至△A′B′C′,使点A′落在BC的延长线上,已知∠A=30°,∠B=40°,则旋转角为( )
如图,将△ABC绕点C按顺时针方向旋转至△A′B′C′,使点A′落在BC的延长线上,已知∠A=30°,∠B=40°,则旋转角为( )| A. | 10° | B. | 35° | C. | 70° | D. | 110° |
15.等腰三角形腰长为5,则其底边长a的取值范围为( )
| A. | 0<a≤5 | B. | 5≤a≤10 | C. | 0<a<10 | D. | 0<a<5 |
2.若a>b,则下列式子正确的是( )
| A. | -2a>-2b | B. | $\frac{a}{2}$<$\frac{b}{2}$ | C. | 4-a<4-b | D. | a-4<b-4 |
12. 如图,△ABC≌△DBE,∠DBC=150°,∠ABD=40°,则∠ABE的度数是( )
如图,△ABC≌△DBE,∠DBC=150°,∠ABD=40°,则∠ABE的度数是( )
 如图,△ABC≌△DBE,∠DBC=150°,∠ABD=40°,则∠ABE的度数是( )
如图,△ABC≌△DBE,∠DBC=150°,∠ABD=40°,则∠ABE的度数是( )| A. | 70° | B. | 65° | C. | 60° | D. | 55° |
19.下列命题正确的是( )
| A. | 对角线相等且互相平分的四边形是矩形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 菱形的面积等于对角线的积 | |
| D. | 平行四边形每条对角线平分一组对角 |
16.某学习小组10名学生参加数学竞赛,他们的得分情况如下表:
那么这10名学生所得分数的众数和中位数分别是( )
| 人数(人) | 2 | 3 | 4 | 1 |
| 分数(分) | 80 | 85 | 90 | 95 |
| A. | 90,90 | B. | 90,85 | C. | 90,87.5 | D. | 85,85 |
17.下列二次根式是最简二次根式的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{10}$ | C. | $\sqrt{12}$ | D. | $\sqrt{18}$ |