��Ŀ����
8���ס������̳����ж�������ijһ��Ʒ����1�����̳�������Ʒ���25%����ۼ�Ϊ1.25Ԫ�������Ʒ�ڼ��̳���ԭ��Ϊ1Ԫ��
��2�����̳����������ַ���������?������Ʒ���20%������?������Ʒ���1Ԫ��ij�˿ͷ��������̳���60ԪǮ�������Ʒ��������?����ļ����ǰ�����?����ļ�����2����10���������Ʒ�����̳���ԭ���Ƕ��٣�
��3���ס������̳��Ѹ���Ʒ����ԭ�۽��������μ۸���������̳�����һ����۵İٷ�����a���ڶ�����۵İٷ�����b�����̳���������۵İٷ��ʶ���$\frac{a+b}{2}$��a��0��b��0��a��b�������ʼס������̳����ĸ��̳�����۽϶ࣿ��˵�����ɣ�
���� ��1�����������г���ʽ�����㼴�ɵõ������
��2�������Ʒ�����̳���ԭ��ΪxԪ�����������г����̣�������̵Ľ�õ�x��ֵ�������鼴�ɵõ������
��3�����������ʾ���������̳���ۺ�ļ۸Ƚϼ��ɵõ������
��� �⣺��1��1.25�£�1+25%��=1��Ԫ����
�ʴ�Ϊ��1��
��2�������Ʒ�����̳���ԭ��ΪxԪ��
��������ã�$\frac{60}{��1+20%��x}$=$\frac{2��60}{x+1}$-10��
��ã�x=1��
�����飺x=1���㷽�̣�����ʵ�ʣ�
�𣺸���Ʒ�����̳���ԭ��Ϊ1Ԫ��
��3������ԭ�۾�Ϊ1Ԫ����
���̳�������ۺ�ļ۸�Ϊ����1+a����1+b��=1+a+b+ab��
���̳�������ۺ�ļ۸�Ϊ����1+$\frac{a+b}{2}$��2=1+a+b+��$\frac{a+b}{2}$��2��
�ߣ�$\frac{a+b}{2}$��2-ab=��$\frac{a-b}{2}$��2��0��
�����̳�������ۺ�۸�϶࣮
���� ���⿼���˷�ʽ���̵�Ӧ�ã�Ū�����еĵ�����ϵ�ǽⱾ��Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
18��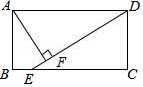 ��ͼ���ھ���ABCD�У�AD��AB������E��BC��һ�㣬��DE=DA��AF��DE������Ϊ��F�������н����У���һ����ȷ���ǣ�������
��ͼ���ھ���ABCD�У�AD��AB������E��BC��һ�㣬��DE=DA��AF��DE������Ϊ��F�������н����У���һ����ȷ���ǣ�������
 ��ͼ���ھ���ABCD�У�AD��AB������E��BC��һ�㣬��DE=DA��AF��DE������Ϊ��F�������н����У���һ����ȷ���ǣ�������
��ͼ���ھ���ABCD�У�AD��AB������E��BC��һ�㣬��DE=DA��AF��DE������Ϊ��F�������н����У���һ����ȷ���ǣ�������| A�� | AF=$\frac{1}{2}$AD | B�� | AB=AF | C�� | ��AFD�ա�DCE | D�� | BE=AD-DF |
19�� ��ͼ����F��E�ֱ����߶�AB��CD�ϣ������������ж�AB��CD���ǣ�������
��ͼ����F��E�ֱ����߶�AB��CD�ϣ������������ж�AB��CD���ǣ�������
 ��ͼ����F��E�ֱ����߶�AB��CD�ϣ������������ж�AB��CD���ǣ�������
��ͼ����F��E�ֱ����߶�AB��CD�ϣ������������ж�AB��CD���ǣ�������| A�� | ��1=��2 | B�� | ��1=��4 | C�� | ��4=��2 | D�� | ��3=��4 |
16��������Ϊx2+7x-18���ǣ�������
| A�� | ��x+2����x-9�� | B�� | ��x-2����x+9�� | C�� | ��x+3����x+9�� | D�� | ��x-3����x+6�� |
3����x��y�������и�ʽ������ȷ���ǣ�������
| A�� | x-6��y-6 | B�� | $\frac{x}{2}$��$\frac{y}{2}$ | C�� | 2x+1��2y+1 | D�� | -x��-y |
13����2m=3��2n=4����23m-2n���ڣ�������
| A�� | $\frac{27}{16}$ | B�� | $\frac{27}{8}$ | C�� | $\frac{9}{8}$ | D�� | 11 |
17��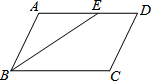 ��ͼ����ƽ���ı���ABCD�У���ABC��ƽ���߽�AD�ڵ�E��AB=4��DE=2����ƽ���ı���ABCD��������Ϊ��������
��ͼ����ƽ���ı���ABCD�У���ABC��ƽ���߽�AD�ڵ�E��AB=4��DE=2����ƽ���ı���ABCD��������Ϊ��������
 ��ͼ����ƽ���ı���ABCD�У���ABC��ƽ���߽�AD�ڵ�E��AB=4��DE=2����ƽ���ı���ABCD��������Ϊ��������
��ͼ����ƽ���ı���ABCD�У���ABC��ƽ���߽�AD�ڵ�E��AB=4��DE=2����ƽ���ı���ABCD��������Ϊ��������| A�� | 12 | B�� | 18 | C�� | 24 | D�� | 32 |
18�� ��ͼ������ABC�Ƶ�C��˳ʱ�뷽����ת����A��B��C�䣬ʹ��A������BC���ӳ����ϣ���֪��A=30�㣬��B=40�㣬����ת��Ϊ��������
��ͼ������ABC�Ƶ�C��˳ʱ�뷽����ת����A��B��C�䣬ʹ��A������BC���ӳ����ϣ���֪��A=30�㣬��B=40�㣬����ת��Ϊ��������
 ��ͼ������ABC�Ƶ�C��˳ʱ�뷽����ת����A��B��C�䣬ʹ��A������BC���ӳ����ϣ���֪��A=30�㣬��B=40�㣬����ת��Ϊ��������
��ͼ������ABC�Ƶ�C��˳ʱ�뷽����ת����A��B��C�䣬ʹ��A������BC���ӳ����ϣ���֪��A=30�㣬��B=40�㣬����ת��Ϊ��������| A�� | 10�� | B�� | 35�� | C�� | 70�� | D�� | 110�� |
