题目内容
9.在平面直角坐标系中,点A在第一象限,点B在x轴正半轴上,∠AOB=60°,OA=8.点A的坐标是( )| A. | (4,8) | B. | (4,4 $\sqrt{3}$) | C. | (4$\sqrt{3}$,4) | D. | (8,4) |
分析 根据直角三角形的性质得出点A的横坐标为4,再用勾股定理得出点A的纵坐标为4$\sqrt{3}$,从而得出答案.
解答 解:∵点A在第一象限,点B在x轴正半轴上,∠AOB=60°,OA=8,
∴点A的横坐标为4,
由勾股定理得点A的纵坐标为$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,
点A坐标(4,4 $\sqrt{3}$),
故选B.
点评 本题考查了坐标与图象的特征,掌握直角三角形的性质以及勾股定理是解题的关键.

练习册系列答案
相关题目
19. 如图,点F,E分别在线段AB和CD上,下列条件能判定AB∥CD的是( )
如图,点F,E分别在线段AB和CD上,下列条件能判定AB∥CD的是( )
 如图,点F,E分别在线段AB和CD上,下列条件能判定AB∥CD的是( )
如图,点F,E分别在线段AB和CD上,下列条件能判定AB∥CD的是( )| A. | ∠1=∠2 | B. | ∠1=∠4 | C. | ∠4=∠2 | D. | ∠3=∠4 |
17.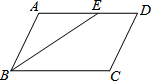 如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=4,DE=2,则平行四边形ABCD的面积最大为( )
如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=4,DE=2,则平行四边形ABCD的面积最大为( )
 如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=4,DE=2,则平行四边形ABCD的面积最大为( )
如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=4,DE=2,则平行四边形ABCD的面积最大为( )| A. | 12 | B. | 18 | C. | 24 | D. | 32 |
4.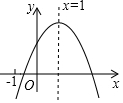 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;
②b>a+c;③9a+3b+c>0; ④c<-3a; ⑤a+b≥m(am+b),其中正确的有( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b>a+c;③9a+3b+c>0; ④c<-3a; ⑤a+b≥m(am+b),其中正确的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
14.函数y=kx-1(常数k>0)的图象不经过的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
1. 如图,D是AB上一点,CB∥ED,EA⊥BA于点A,若∠ABC=38°,则∠AED的度数为( )
如图,D是AB上一点,CB∥ED,EA⊥BA于点A,若∠ABC=38°,则∠AED的度数为( )
 如图,D是AB上一点,CB∥ED,EA⊥BA于点A,若∠ABC=38°,则∠AED的度数为( )
如图,D是AB上一点,CB∥ED,EA⊥BA于点A,若∠ABC=38°,则∠AED的度数为( )| A. | 38° | B. | 48° | C. | 52° | D. | 62° |
18. 如图,将△ABC绕点C按顺时针方向旋转至△A′B′C′,使点A′落在BC的延长线上,已知∠A=30°,∠B=40°,则旋转角为( )
如图,将△ABC绕点C按顺时针方向旋转至△A′B′C′,使点A′落在BC的延长线上,已知∠A=30°,∠B=40°,则旋转角为( )
 如图,将△ABC绕点C按顺时针方向旋转至△A′B′C′,使点A′落在BC的延长线上,已知∠A=30°,∠B=40°,则旋转角为( )
如图,将△ABC绕点C按顺时针方向旋转至△A′B′C′,使点A′落在BC的延长线上,已知∠A=30°,∠B=40°,则旋转角为( )| A. | 10° | B. | 35° | C. | 70° | D. | 110° |
19.下列命题正确的是( )
| A. | 对角线相等且互相平分的四边形是矩形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 菱形的面积等于对角线的积 | |
| D. | 平行四边形每条对角线平分一组对角 |
