题目内容
6. 如图,两条宽度都是1的纸条,交叉重叠放在一起,且夹角为α,则重叠部分的面积为( )
如图,两条宽度都是1的纸条,交叉重叠放在一起,且夹角为α,则重叠部分的面积为( )| A. | $\frac{1}{sinα}$ | B. | $\frac{1}{cosα}$ | C. | tanα | D. | 1 |
分析 首先过A作AE⊥BC,AF⊥CD于F,垂足为E,F,证明BC=CD,从而证明四边形ABCD是菱形,再利用三角函数算出BC的长,最后根据菱形的面积公式算出重叠部分的面积即可.
解答 解: 如图所示:过A作AE⊥BC,AF⊥CD于F,垂足为E,F,
如图所示:过A作AE⊥BC,AF⊥CD于F,垂足为E,F,
∴∠AEB=∠AFD=90°,
∵AD∥CB,AB∥CD,
∴四边形ABCD是平行四边形,
∵纸条宽度都为1,
∴AE=AF=1,
∵平行四边形的面积=BC•AE=CD•AF,∴BC=CD,
∴四边形ABCD是菱形.
∴BC=AB,
∵$\frac{AE}{AB}$=sinα,
∴BC=AB=$\frac{AE}{sinα}$=$\frac{1}{sinα}$,
∴重叠部分(图中阴影部分)的面积=BC×AE=$\frac{1}{sinα}$×1=$\frac{1}{sinα}$.
故选:A.
点评 此题主要考查了菱形的判定与性质,以及三角函数的应用,关键是证明四边形ABCD是菱形,利用三角函数求出BC的长.

练习册系列答案
相关题目
16.计算结果为x2+7x-18的是( )
| A. | (x+2)(x-9) | B. | (x-2)(x+9) | C. | (x+3)(x+9) | D. | (x-3)(x+6) |
17.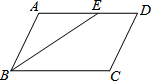 如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=4,DE=2,则平行四边形ABCD的面积最大为( )
如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=4,DE=2,则平行四边形ABCD的面积最大为( )
 如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=4,DE=2,则平行四边形ABCD的面积最大为( )
如图,在平行四边形ABCD中,∠ABC的平分线交AD于点E,AB=4,DE=2,则平行四边形ABCD的面积最大为( )| A. | 12 | B. | 18 | C. | 24 | D. | 32 |
14.函数y=kx-1(常数k>0)的图象不经过的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
1. 如图,D是AB上一点,CB∥ED,EA⊥BA于点A,若∠ABC=38°,则∠AED的度数为( )
如图,D是AB上一点,CB∥ED,EA⊥BA于点A,若∠ABC=38°,则∠AED的度数为( )
 如图,D是AB上一点,CB∥ED,EA⊥BA于点A,若∠ABC=38°,则∠AED的度数为( )
如图,D是AB上一点,CB∥ED,EA⊥BA于点A,若∠ABC=38°,则∠AED的度数为( )| A. | 38° | B. | 48° | C. | 52° | D. | 62° |
11. 如图,将一张矩形的纸对折,旋转90°后再对折,然后沿着右图中的虚线剪下,则剪下的纸片打开后的形状一定为( )
如图,将一张矩形的纸对折,旋转90°后再对折,然后沿着右图中的虚线剪下,则剪下的纸片打开后的形状一定为( )
 如图,将一张矩形的纸对折,旋转90°后再对折,然后沿着右图中的虚线剪下,则剪下的纸片打开后的形状一定为( )
如图,将一张矩形的纸对折,旋转90°后再对折,然后沿着右图中的虚线剪下,则剪下的纸片打开后的形状一定为( )| A. | 三角形 | B. | 菱形 | C. | 矩形 | D. | 正方形 |
18. 如图,将△ABC绕点C按顺时针方向旋转至△A′B′C′,使点A′落在BC的延长线上,已知∠A=30°,∠B=40°,则旋转角为( )
如图,将△ABC绕点C按顺时针方向旋转至△A′B′C′,使点A′落在BC的延长线上,已知∠A=30°,∠B=40°,则旋转角为( )
 如图,将△ABC绕点C按顺时针方向旋转至△A′B′C′,使点A′落在BC的延长线上,已知∠A=30°,∠B=40°,则旋转角为( )
如图,将△ABC绕点C按顺时针方向旋转至△A′B′C′,使点A′落在BC的延长线上,已知∠A=30°,∠B=40°,则旋转角为( )| A. | 10° | B. | 35° | C. | 70° | D. | 110° |
15.等腰三角形腰长为5,则其底边长a的取值范围为( )
| A. | 0<a≤5 | B. | 5≤a≤10 | C. | 0<a<10 | D. | 0<a<5 |
16.某学习小组10名学生参加数学竞赛,他们的得分情况如下表:
那么这10名学生所得分数的众数和中位数分别是( )
| 人数(人) | 2 | 3 | 4 | 1 |
| 分数(分) | 80 | 85 | 90 | 95 |
| A. | 90,90 | B. | 90,85 | C. | 90,87.5 | D. | 85,85 |