题目内容
18.仔细阅读下面例题,解答问题:例题:已知二次三项式x2-4x+m分解因式后有一个因式是(x+3),求另一个因式以及m的值.
解:方法一:设另一个因式为(x+n),得x2-4x+m=(x+3)(x+n),则x2-4x+m=x2+(n+3)x+3n,∴$\left\{\begin{array}{l}{n+3=-4}\\{m=3n}\end{array}\right.$,解得:n=-7,m=-21,∴另一个因式为(x-7),m的值为-21.
方法二:设x2-4x+m=k(x+3)(k≠0),当x=-3时,左边=(-3)2-4(-3)+m,右边=0,∴(-3)2-4(-3)+m=0,解得:m=-21,x2-4x+m=x2-4x-21=(x-7)(x+3),∴n=-7∴另一个因式为(x-7),m的值为-21.
仿照以上方法一或方法二解答下面2个问题:
(1)已知二次三项式8x2-14x-k分解因式后有一个因式是(2x-3),求另一个因式以及k的值;
(2)已知三次四项式ax3-x2-4x+c分解因式后有2个因式分别是(x-1)与(x+2),求这个多项式分解因式后的第3个因式以及a,c的值.
分析 (1)先将8x2-14x-k解成一个因式是(2x-3),设另一个因式是(4x+b),则(2x-3)(4x+b)=8x2+2bx-12x-3b=8x2+(2b-12)x-3b=8x2-14x-k,根据对应项的系数相等即可求得b和k的值;
(2)根据已知二次三项式因式分解的结果,推理表示出第3个因式,利用多项式乘以多项式法则计算,利用多项式相等的条件求出a与c的值,即可确定出第3个因式.
解答 解:(1)设另一个因式是(4x+b),则(2x-3)(4x+b)=8x2+2bx-12x-3b=8x2+(2b-12)x-3b=8x2-14x-k,
$\left\{\begin{array}{l}{2b-12=-14}\\{3b=k}\end{array}\right.$,
解得:b=-1,k=-3,
因此另一个因式是4x-1,k=-3.
(2)根据题意得:ax3-x2-4x+c=(ax-$\frac{1}{2}$c)(x-1)(x+2)=(ax-$\frac{1}{2}$c)(x2+x-2)=ax3+(a-$\frac{1}{2}$c)x2-(2a+$\frac{1}{2}$c)x+c,
可得a-$\frac{1}{2}$c=-1,2a+$\frac{1}{2}$c=4,
解得:a=1,c=4,
则第3个因式为(x-2),a=1,c=4.
点评 本题考查了因式分解的意义,正确理解因式分解与整式的乘法互为逆运算是关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
8.若a2-3ab-4b2=0,则$\frac{a}{b}$的值( )
| A. | 1 | B. | -1 | C. | 4或-1 | D. | -4或1 |
 如图,在直角坐标系中,∠AOx=60°,∠BOx=135°,OA=2,OB=$\sqrt{2}$,一次函数的图象经过A,B两点,求这个一次函数的表达式.
如图,在直角坐标系中,∠AOx=60°,∠BOx=135°,OA=2,OB=$\sqrt{2}$,一次函数的图象经过A,B两点,求这个一次函数的表达式.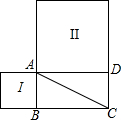 如图,矩形ABCD的对角线AC=6cm,分别以AB和AD为一边向外作正方形Ⅰ和Ⅱ,则正方形Ⅰ和Ⅱ的面积之和是多少?
如图,矩形ABCD的对角线AC=6cm,分别以AB和AD为一边向外作正方形Ⅰ和Ⅱ,则正方形Ⅰ和Ⅱ的面积之和是多少? 如图,在Rt△ABC中,∠C=90°,AC:BC=1:2,在Rt△ABC中有多个依次排队的正方形DCFE,GFHK,PHTQ…,如果第一个正方形的边长为a,则第2012个正方形的边长应为$\frac{{2}^{2012}}{{3}^{2012}}$.
如图,在Rt△ABC中,∠C=90°,AC:BC=1:2,在Rt△ABC中有多个依次排队的正方形DCFE,GFHK,PHTQ…,如果第一个正方形的边长为a,则第2012个正方形的边长应为$\frac{{2}^{2012}}{{3}^{2012}}$.