题目内容
8. 如图,在Rt△ABC中,∠C=90°,AC:BC=1:2,在Rt△ABC中有多个依次排队的正方形DCFE,GFHK,PHTQ…,如果第一个正方形的边长为a,则第2012个正方形的边长应为$\frac{{2}^{2012}}{{3}^{2012}}$.
如图,在Rt△ABC中,∠C=90°,AC:BC=1:2,在Rt△ABC中有多个依次排队的正方形DCFE,GFHK,PHTQ…,如果第一个正方形的边长为a,则第2012个正方形的边长应为$\frac{{2}^{2012}}{{3}^{2012}}$.
分析 根据相似三角形的性质求出第一个,第二个,第三个正方形的边长的值,找出规律即可求出第2012个正方形的边长.
解答 解:∵∠C=90°,AC:BC=1:2,
设AC=1,BC=2,
在正方形DCFE中,∵DE∥BC,∴△ADE∽△BCA,
∴$\frac{AD}{AC}=\frac{DE}{BC}$,即$\frac{1-a}{1}$=$\frac{a}{2}$,
∴a=$\frac{2}{3}$;
同理,∵GK∥BC,∴△EGK∽△BEF,
∴$\frac{EG}{EF}=\frac{GK}{BF}$,即$\frac{\frac{2}{3}-GK}{\frac{2}{3}}$=$\frac{GK}{2-\frac{2}{3}}$,
∴GK=$\frac{4}{9}$=($\frac{2}{3}$)2;
同理可求出PQ=$\frac{{2}^{3}}{{3}^{3}}$.
∴第2012个正方形的边长=$\frac{{2}^{2012}}{{3}^{2012}}$.
故答案为:$\frac{{2}^{2012}}{{3}^{2012}}$.
点评 本题考查了正方形的性质,相似三角形的判定与性质,解题的关键是根据相似三角形对应边成比例找出后面正方形的边长与第一个正方形的边长的关系.

练习册系列答案
相关题目
20.九年级(1)班体检结果出来后,一位同学对全班同学的身高(单位:厘米)统计如表:
这组数据的众数为( )
| 身高(厘米) | 158 | 160 | 162 | 165 | 167 | 170 |
| 人数 | 2 | 5 | 8 | 18 | 10 | 7 |
| A. | 158 | B. | 162 | C. | 165 | D. | 167 |
 如图,AB=AD,AC=AE,∠BAD=∠CAE=90°,点F为DE的中点,求证:BC=2AF.
如图,AB=AD,AC=AE,∠BAD=∠CAE=90°,点F为DE的中点,求证:BC=2AF.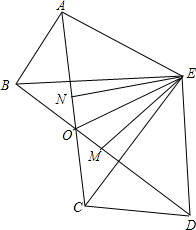 如图,BE=CE,AB=DC,∠ABE=∠DCE,连接AC、DB交于点O,连接OE,EM、EN分别平分∠AEC和∠BED.求证:
如图,BE=CE,AB=DC,∠ABE=∠DCE,连接AC、DB交于点O,连接OE,EM、EN分别平分∠AEC和∠BED.求证: