题目内容

6．已知$\left\{\begin{array}{l}{a+2b=3c}\\{2a-3b=-8c}\end{array}\right.$，求$\frac{3a+4b+c}{4a-3b+2c}$的值．

分析 把方程组$\left\{\begin{array}{l}{a+2b=3c①}\\{2a-3b=-8c②}\end{array}\right.$看作关于a、b的二元一次方程组，利用加减消元法可求出b=2c，再利用代入法得到a=-c，然后把a=-c，b=2c代入代数式中进行分式的计算即可．
把b=2c代入①得a+4c=3c，

解答 解：$\left\{\begin{array}{l}{a+2b=3c①}\\{2a-3b=-8c②}\end{array}\right.$，
①×2-②得4b+3b=6c+8c，
解得b=2c，
把b=2c代入①得a+4c=3c，
解得a=-c，
所以原式=$\frac{-3c+8c+c}{-4c-4c+2c}$=-1．

点评 本题考查了解三元一次方程组：利用代入消元法或加减消元法把解三元一次方程组的问题转化为解二元一次方程组的问题．也考查了分式的值．

练习册系列答案
相关题目
16．计算：2cos45°+（$\sqrt{2}$-1）0-（$\frac{1}{2}$）-2+$\root{3}{8}$．
17．解方程组：$\left\{\begin{array}{l}{5x+6y=-7}\\{7x-9y=25}\end{array}\right.$．
14．已知线段x是线段a和线段b的比例中项，且线段x是线段a与线段b的和的一半，则$\frac{a}{b}$的值等于（　　）
A．$\frac{\sqrt{2}}{2}$B．$\frac{1}{4}$C．$\frac{2}{3}$D．1
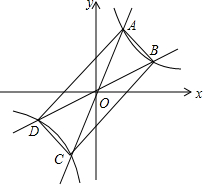1．求证：无论k为何值，y2+2xy-x2+2x-2ky+k2+1都不能分解成两个一次因式的乘积．
11．如图，过原点的直线y=k1x和y=k2x与反比例函数y=$\frac{1}{x}$的图象分别交于两点A，C和B，D，连接AB，BC，CD，DA．
（1）四边形ABCD一定是平行四边形（直接填写结果）．
（2）四边形ABCD可能是矩形吗？若可能，试求此时k1和k2之间的关系式；若不可能，说明理由．
18．仔细阅读下面例题，解答问题：
例题：已知二次三项式x2-4x+m分解因式后有一个因式是（x+3），求另一个因式以及m的值．
解：方法一：设另一个因式为（x+n），得x2-4x+m=（x+3）（x+n），则x2-4x+m=x2+（n+3）x+3n，∴$\left\{\begin{array}{l}{n+3=-4}\\{m=3n}\end{array}\right.$，解得：n=-7，m=-21，∴另一个因式为（x-7），m的值为-21．
方法二：设x2-4x+m=k（x+3）（k≠0），当x=-3时，左边=（-3）2-4（-3）+m，右边=0，∴（-3）2-4（-3）+m=0，解得：m=-21，x2-4x+m=x2-4x-21=（x-7）（x+3），∴n=-7∴另一个因式为（x-7），m的值为-21．
仿照以上方法一或方法二解答下面2个问题：
（1）已知二次三项式8x2-14x-k分解因式后有一个因式是（2x-3），求另一个因式以及k的值；
（2）已知三次四项式ax3-x2-4x+c分解因式后有2个因式分别是（x-1）与（x+2），求这个多项式分解因式后的第3个因式以及a，c的值．
15．一套《木偶奇遇记》共16本，每本单价相同，新年期间甲、乙两书店出售这套丛书时采取了不同的促销方法（如下），请你给大家支个招，若买一套书，到哪个书店买更便宜．
甲书店：全场一律打八折出售；
乙书店：买3本赠送1本，不足3本按原价出售．
16．如图，AB=AD，AC=AE，∠BAD=∠CAE=90°，点F为DE的中点，求证：BC=2AF．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网