题目内容
如果记函数f(x)=
,并且f(1)表示当x=1时对应的函数值,即f(1)=
=
;f(
)表示当x=
时,y的值,即f(
)=
=
,…,则f(1)+f(2)+f(
)+f(3)+f(
)+…+f(
)+f(2012)的值= .
| x2 |
| 1+x2 |
| 12 |
| 1+12 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(
| ||
1+(
|
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2012 |
考点:函数值
专题:新定义,规律型
分析:由f(x)=
,可得f(2)=
=
;又f(
)=
=
,那么f(2)+f(
)=1,同理,f(3)+f(
)=1,…,f(
)+f(2012)=1,进而求解即可.
| x2 |
| 1+x2 |
| 22 |
| 1+22 |
| 4 |
| 5 |
| 1 |
| 2 |
(
| ||
1+(
|
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2012 |
解答:解:∵f(x)=
,
∴f(2)=
=
,f(
)=
=
,
∴f(2)+f(
)=1,
同理,f(3)+f(
)=1,
…,
f(
)+f(2012)=1,
∵f(1)=
=
,
∴f(1)+f(2)+f(
)+f(3)+f(
)+…+f(
)+f(2012)
=
+1×2011
=2011
.
故答案为2011
.
| x2 |
| 1+x2 |
∴f(2)=
| 22 |
| 1+22 |
| 4 |
| 5 |
| 1 |
| 2 |
(
| ||
1+(
|
| 1 |
| 5 |
∴f(2)+f(
| 1 |
| 2 |
同理,f(3)+f(
| 1 |
| 3 |
…,
f(
| 1 |
| 2012 |
∵f(1)=
| 12 |
| 1+12 |
| 1 |
| 2 |
∴f(1)+f(2)+f(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2012 |
=
| 1 |
| 2 |
=2011
| 1 |
| 2 |
故答案为2011
| 1 |
| 2 |
点评:本题考查了函数值,解答此题关键是根据题中所给的式子找出规律,再解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△ABC中,DE∥BC,AD:AB=1:3,若△ADE的面积等于2,则△ABC的面积等于( )
如图,在△ABC中,DE∥BC,AD:AB=1:3,若△ADE的面积等于2,则△ABC的面积等于( )| A、6 | B、8 | C、12 | D、18 |
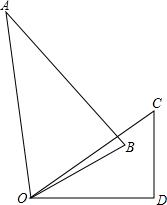 将一副含有60°角的三角板ABO的顶点O和另一块含有45°角的三角板CO′D的顶点O′重合,绕点O旋转三角板ABO,拼成如图情况,问:是否存在∠AOC,有∠AOC=3∠BOD?如果存在,求出∠AOD的度数,如果不存在,请说明理由.
将一副含有60°角的三角板ABO的顶点O和另一块含有45°角的三角板CO′D的顶点O′重合,绕点O旋转三角板ABO,拼成如图情况,问:是否存在∠AOC,有∠AOC=3∠BOD?如果存在,求出∠AOD的度数,如果不存在,请说明理由.