题目内容

如图，在△ABC中，DE∥BC，AD：AB=1：3，若△ADE的面积等于2，则△ABC的面积等于（　　）
A、6B、8C、12D、18
考点：相似三角形的判定与性质
专题：
分析：由条件证明△ADE∽△ABC，且相似比为
1
3
，再利用相似三角形的性质可求得△ABC的面积．
解答：解：
∵DE∥BC，
∴△ADE∽△ABC，
∴
S△ADE
S△ABC
=（
AD
AB
）2=（
1
3
）2=
1
9
，
∵S△ADE=2，
∴
2
S△ABC
=
1
9
，解得S△ABC=18，
故选D．
点评：本题主要考查相似三角形的判定和性质，掌握相似三角形的面积比等于相似比的平方是解题的关键．
练习册系列答案
相关题目
下列各分式当x取何值时分式有意义？
（1）
x+1
x-1
；
（2）
2
x2-1
；
（3）
x-y
x2+2
．
分解因式：
（1）（m2+2m）2-2m2-4m+1．
（2）a2+b2-c2-2ab．
因式分解：（a+b）2-（ab+1）2．
计算：(
3
-1)0-
(-3)2
．
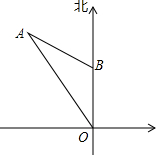如图，某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向，且与O相距20
3
千米的A处；经过40分钟，又测得该轮船位于O的正北方向，且与O相距20千米的B处，求该轮船的航行速度．
因式分解：
①
1
4
x+x3-x2；
②4a2（x-y）3+b2（y-x）3．
如果记函数f（x）=
x2
1+x2
，并且f（1）表示当x=1时对应的函数值，即f（1）=
12
1+12
=
1
2
；f（
1
2
）表示当x=
1
2
时，y的值，即f（
1
2
）=
(
1
2
)2
1+(
1
2
)2
=
1
5
，…，则f（1）+f（2）+f（
1
2
）+f（3）+f（
1
3
）+…+f（
1
2012
）+f（2012）的值=
 
．
解方程：
x
x-1
=1+
2
x
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网