题目内容
已知二次函数y=x2+(m+1)x-2m2-m.
(1)证明:无论m为何值,函数图象与x轴都有交点;
(2)当图象的对称轴为直线x=1时,求它与坐标轴的三个交点所围成的三角形的面积.
(1)证明:无论m为何值,函数图象与x轴都有交点;
(2)当图象的对称轴为直线x=1时,求它与坐标轴的三个交点所围成的三角形的面积.
考点:抛物线与x轴的交点
专题:
分析:(1)判断函数图象与x轴的交点情况,就要列出判别式,用配方法确定判别式大于0;
(2)已知对称轴,可以用对称轴的公式求出本题中的待定系数,确定函数解析式,再根据图象求面积.
(2)已知对称轴,可以用对称轴的公式求出本题中的待定系数,确定函数解析式,再根据图象求面积.
解答:(1)证明:∵b2-4ac=(m+1)2-4(-2m2-m)=(3m+1)2≥0,
∴无论m取何值,函数图象与x轴都有交点;
(2)解:由对称轴x=1得:-
=1,
解得m=-3,
∴二次函数为y=x2-2x-15=(x-5)(x+3).
∴与x轴的两交点是(0,5),(0,-3),与y轴的交点为(0,-15),
∴它与坐标轴的三个交点所围成的三角形的面积为:
×8×15=60.
∴无论m取何值,函数图象与x轴都有交点;
(2)解:由对称轴x=1得:-
| m+1 |
| 2 |
解得m=-3,
∴二次函数为y=x2-2x-15=(x-5)(x+3).
∴与x轴的两交点是(0,5),(0,-3),与y轴的交点为(0,-15),
∴它与坐标轴的三个交点所围成的三角形的面积为:
| 1 |
| 2 |
点评:本题考查了抛物线与x轴的交点.解答此题的关键是根据对称轴的公式求待定系数,然后由图象解答求面积的问题,锻炼了学生数形结合的思想方法.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
 如图,已知D,E分别是△ABC的AB,AC边上的点,DE∥BC,AM⊥BC,垂足为N,AM与DE相交于点N,S△ADE:S四边形DBCE=1:8,求AN:AM.
如图,已知D,E分别是△ABC的AB,AC边上的点,DE∥BC,AM⊥BC,垂足为N,AM与DE相交于点N,S△ADE:S四边形DBCE=1:8,求AN:AM.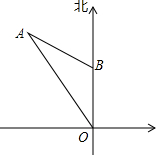 如图,某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距20
如图,某时刻测得一艘匀速直线航行的轮船位于O的北偏西30°方向,且与O相距20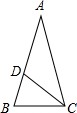 如图,在△ABC中,∠A=36°,∠B=72°,CD是∠ACD的平分线,则图中共有
如图,在△ABC中,∠A=36°,∠B=72°,CD是∠ACD的平分线,则图中共有 已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BC=EF.
已知:如图,点B,E,C,F在同一直线上,AB∥DE,且AB=DE,BC=EF.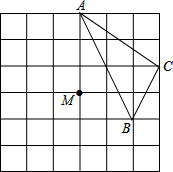 如图,6×6的网格中,每个小正方形的边长为1.
如图,6×6的网格中,每个小正方形的边长为1.