题目内容
19.在△ABC中,AB=BC,BD⊥AC于点D.(1)如图1,当∠ABC=90°时,若CE平分∠ACB,交AB于点E,交BD于点F.
①求证:△BEF是等腰三角形;
②求证:BD=$\frac{1}{2}$(BC+BF);
(2)点E在AB边上,连接CE.若BD=$\frac{1}{2}$(BC+BE),在图2中补全图形,判断∠ACE与∠ABC之间的数量关系,写出你的结论,并写出求解∠ACE与∠ABC关系的思路.

分析 (1)①根据∠ABC=90°,∠FDC=90°,以及∠ECB=∠ACE=22.5°,即可得到∠BEF=∠CFD=∠BFE=67.5°,即可判定△BEF是等腰三角形;
②延长AB至M,使得BM=AB,连接CM,根据三角形中位线定理可得BD∥CM,BD=$\frac{1}{2}$CM,再根据∠BFE=∠MCE=∠BEF,可得EM=MC,进而得出BD=$\frac{1}{2}$EM=$\frac{1}{2}$(BC+BF);
(2)与(1)②同理可得BD∥PC,BD=$\frac{1}{2}$PC,BP=BC;由BD=$\frac{1}{2}$(BC+BE),可证明△PEC和△BEF分别是等腰三角形;由∠BEF+∠BFE+∠EBF=180°以及∠FCD+∠DFC=90°,可得$\frac{180°-∠EBF}{2}$=90°-∠DCF,即可得到∠ACE与∠ABC之间的数量关系:∠ACE=$\frac{1}{4}$∠ABC.
解答  解:(1)①在△ABC中,AB=BC,BD⊥AC于点D,
解:(1)①在△ABC中,AB=BC,BD⊥AC于点D,
∴∠ABD=∠CBD,AD=CD,
∵∠ABC=90°,
∴∠ACB=45°,
∵CE平分∠ACB,
∴∠ECB=∠ACE=22.5°,
∴∠BEF=∠CFD=∠BFE=67.5°,
∴BE=BF,
∴△BEF是等腰三角形;
②如图,延长AB至M,使得BM=AB,连接CM,
∴BD∥CM,BD=$\frac{1}{2}$CM,
∴∠BCM=∠DBC=∠ABD=∠BMC=45°,
∠BFE=∠MCE,
∴BC=BM,
由①得,∠BEF=∠BFE,BE=BF,
∴∠BFE=∠MCE=∠BEF,
∴EM=MC,
∴BD=$\frac{1}{2}$EM=$\frac{1}{2}$(BC+BF);
(2)∠ACE=$\frac{1}{4}$∠ABC.
求解∠ACE与∠ABC关系的思路:
a,延长AB至P,使得BP=AB,连接CP,与(1)②同理可得BD∥PC,BD=$\frac{1}{2}$PC,BP=BC;
b,由BD=$\frac{1}{2}$(BC+BE),可证明△PEC和△BEF分别是等腰三角形;
c,由∠BEF+∠BFE+∠EBF=180°以及∠FCD+∠DFC=90°,可得$\frac{180°-∠EBF}{2}$=90°-∠DCF,即可证明∠ACE=$\frac{1}{4}$∠ABC.
点评 本题主要考查了全等三角形的判定与性质,等腰三角形的判定与性质以及等腰直角三角形的性质的运用,解决问题的关键是作辅助线,构造等腰三角形.

| A. | 2016x | B. | x+2016 | C. | |2016x| | D. | |x|+2016 |
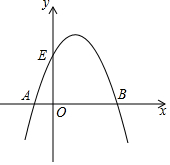 已知抛物线经过点A(-1,0),B(3,0),C(1,4),与y轴交于点E.
已知抛物线经过点A(-1,0),B(3,0),C(1,4),与y轴交于点E.
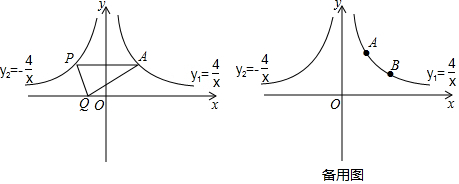
 如图,等边△AOB中点O是原点,点A在y轴上,点B的坐标是(2$\sqrt{3}$,2),小明做一个数学实验,在x轴上取一动点C,以AC为一边画出等边△ACP,移动点C时,探究点P的位置变化情况.
如图,等边△AOB中点O是原点,点A在y轴上,点B的坐标是(2$\sqrt{3}$,2),小明做一个数学实验,在x轴上取一动点C,以AC为一边画出等边△ACP,移动点C时,探究点P的位置变化情况.
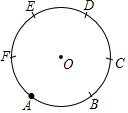 尺规作图特有的魅力曾使无数人沉湎其中,连当年叱咤风云的拿破仑也不例外,我们可以只用圆规将圆等分.例如可将圆6等分,如图只需在⊙O上任取点A,从点A开始,以⊙O的半径为半径,在⊙O上依次截取点B,C,D,E,F.从而点A,B,C,D,E,F把⊙O六等分.下列可以只用圆规等分的是( )
尺规作图特有的魅力曾使无数人沉湎其中,连当年叱咤风云的拿破仑也不例外,我们可以只用圆规将圆等分.例如可将圆6等分,如图只需在⊙O上任取点A,从点A开始,以⊙O的半径为半径,在⊙O上依次截取点B,C,D,E,F.从而点A,B,C,D,E,F把⊙O六等分.下列可以只用圆规等分的是( )