题目内容
11.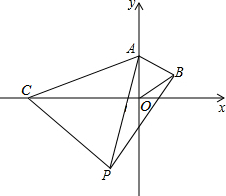 如图,等边△AOB中点O是原点,点A在y轴上,点B的坐标是(2$\sqrt{3}$,2),小明做一个数学实验,在x轴上取一动点C,以AC为一边画出等边△ACP,移动点C时,探究点P的位置变化情况.
如图,等边△AOB中点O是原点,点A在y轴上,点B的坐标是(2$\sqrt{3}$,2),小明做一个数学实验,在x轴上取一动点C,以AC为一边画出等边△ACP,移动点C时,探究点P的位置变化情况.(1)如图,小明将点C移至x轴负半轴,在AC的右侧画出等边△ACP,并使得顶点P在第三象限时,连接BP,求证:△AOC≌△ABP;
(2)小明在x轴上移动点C,并在AC的右侧画出等边△ACP时,发现点P在某函数图象上,请求出点P所在函数图象的解析式.
(3)小明在x轴上移动点C点时,若在AC的左侧画出等边△ACP,点P会不会在某函数图象上?若会在某函数图象上,请直接写出该函数图象的解析式,若不在某函数图象上,请说明理由.
分析 (1)利用等边三角形的性质,根据SAS根据解决问题.
(2)首先证明点P在过点A且与AB垂直的直线上,求出特殊点(P在y轴上的点),利用待定系数法即可解决问题.
(3)如图作B的对称点B′,连接AB′,OB′.由(2)可知,P′B′⊥AB′,同法可得直线P′B′的解析式为t=-$\sqrt{3}$x-4.
解答 (1)证明:如图,
∵△AOB与△ACP都是等边三角形,
∴OA=AB,A=AP,CAP=∠OAB=60°.
∴∠CAP+∠PAO=∠OAB+∠PAO.
∴∠CAO=∠PAB.
在△AOC与△PAB中,
$\left\{\begin{array}{l}{AO=AB}\\{∠CAO=∠PAB}\\{AC=AP}\end{array}\right.$,
∴△AOC≌△ABP.
(2)解:由(1)可知,△AOC≌△ABP,
∴∠COA=∠PBA=90°,
∴点P在过点B且与AB垂直的直线上,
在等边△AOB中,B(2$\sqrt{3}$,2),
∴AB=4,
当点C移动,使得P在y轴上时,
∵△PAB是直角三角形,∠PAB=60°,
∴PA=$\frac{AB}{cos60°}$=8,
∴P(0,-4),
设直线PB的解析式为y=kx-4,把B(2$\sqrt{3}$,2)代入得到k=$\sqrt{3}$,
∴点P所在函数图象的解析式为y=$\sqrt{3}$x-4.
(3)会在函数的图象上,如图作B的对称点B′,连接AB′,OB′.
由(2)可知,P′B′⊥AB′,同法可得直线P′B′的解析式为t=-$\sqrt{3}$x-4.
∴该函数图象的解析式为y=-$\sqrt{3}$x-4.
点评 本题考查三角形综合题、等边三角形的性质、全等三角形的判定和性质、一次函数的应用等知识,解题的关键是正确寻找全等三角形解决问题,学会添加常用辅助线,其中全等三角形,熟练正确待定系数法确定函数解析式,属于中考压轴题.

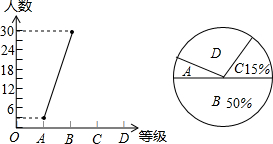 为迎接常熟市文明城市创建工作,某校八年级一班开展了“社会主义核心价值观、未成年人基本文明礼仪规范”的知识竞赛活动,成绩分为A、B、C、D四个等级,并将收集的数据绘制了两幅不完整的统计图.请你根据图中所给出的信息,解答下列各题:
为迎接常熟市文明城市创建工作,某校八年级一班开展了“社会主义核心价值观、未成年人基本文明礼仪规范”的知识竞赛活动,成绩分为A、B、C、D四个等级,并将收集的数据绘制了两幅不完整的统计图.请你根据图中所给出的信息,解答下列各题:
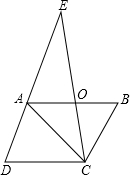 如图,△ABC中,∠B=58°,AB∥CD,∠ADC=∠DAC,∠ACB的平分线交DA的延长线于点E,则∠E的度数为29°.
如图,△ABC中,∠B=58°,AB∥CD,∠ADC=∠DAC,∠ACB的平分线交DA的延长线于点E,则∠E的度数为29°.