题目内容
8.在平面直角坐标系中,点A(-4,0),B(0,3),将线段AB向右平移m(m为正数)个单位向下平移1个单位长度到CD,点A、B的对应点分别为C、D.(1)直接写出点C(-4+m,-1),D(m,2)(用含m的式子表示);
(2)连接AC、AD,若三角形ACD面积是三角形ABO面积的2倍,求m的值;
(3)如图2,在线段OA上取一点E(不与O、A重合),F为y轴负半轴上一点,且FD平分∠CDE,若∠ABE=∠DEO,∠BED=α,求∠ABE+2∠BFD的度数(结果用含α的式子表示).
分析 (1)构建点平移的性质,即可写出C、D两点坐标;
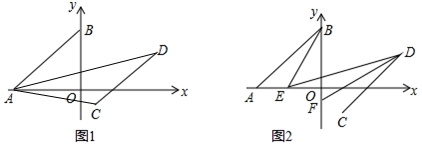
(2)如图1中,过点C作MN∥x轴,作AM⊥MN,DN⊥MN.构建方程即可解决问题;
(3)如图2中,作EH∥AB,连接DO延长到G,.设∠ABE=∠DEO=y,∠FDE=∠FDC=x,∠BFD=z.想办法构建方程组即可解决问题.
解答 解:(1)∵点A(-4,0),B(0,3),将线段AB向右平移m(m为正数)个单位向下平移1个单位长度到CD,
∴C(-4+m,-1),D(m,2),
故答案为-4+m,-1,m,2.
(2)如图1中,过点C作MN∥x轴,作AM⊥MN,DN⊥MN.
由题意:$\frac{1}{2}$(1+3)•(m+4)-$\frac{1}{2}$•m•1-$\frac{1}{2}$•4•3=2•$\frac{1}{2}$•3•4,
解得m=$\frac{20}{3}$.
(3)如图2中,作EH∥AB,连接DO延长到G,.设∠ABE=∠DEO=y,∠FDE=∠FDC=x,∠BFD=z.
∵AB∥CD,
∴AB∥EH∥CD,
∴∠ABE=∠BEH,∠HED=∠EDC,
∴∠BED=∠ABE+∠EDC,
∴α=y+2x ①
∵∠EOG=∠DEO+∠EDO,∠GOF=∠BFD+∠ODF,
∴∠EOF=∠DEO+∠EDF+∠BFD,
∴x+y+z=90° ②
由①②可得y+2z=180°-α,
∴∠ABE+2∠BFD=180°-α.
点评 本题考查三角形综合题、平行线的性质、三角形的面积、三角形内角和定理,三角形的外角的性质等知识,解题的关键是学会用构建方程的思想思考问题,属于中考压轴题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
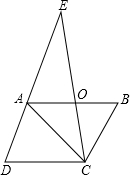
 已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,过点B作BK⊥AC,垂足为K,过D作DH∥KB,DH分别与AC,AB,⊙O及CB的延长线相交于点E,F,G,H,且F是EG的中点.
已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,过点B作BK⊥AC,垂足为K,过D作DH∥KB,DH分别与AC,AB,⊙O及CB的延长线相交于点E,F,G,H,且F是EG的中点.
 如图,△ABC中,∠B=58°,AB∥CD,∠ADC=∠DAC,∠ACB的平分线交DA的延长线于点E,则∠E的度数为29°.
如图,△ABC中,∠B=58°,AB∥CD,∠ADC=∠DAC,∠ACB的平分线交DA的延长线于点E,则∠E的度数为29°.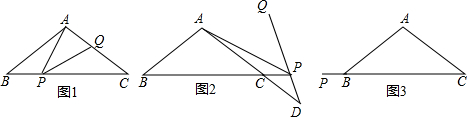
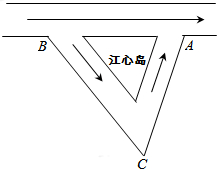 如图,已知箭头的方向是水流的方向,一艘游艇从江心岛的右侧A点逆流航行3小时到达B点后,又继续顺流航行2.5小时到达C点,总共行驶了208千米,已知游艇在静水中的速度是38千米/小时.
如图,已知箭头的方向是水流的方向,一艘游艇从江心岛的右侧A点逆流航行3小时到达B点后,又继续顺流航行2.5小时到达C点,总共行驶了208千米,已知游艇在静水中的速度是38千米/小时.