题目内容
6. 点A在函数y=-$\frac{2}{x}$(x<0)的图象上,点B在y=$\frac{3}{x}$(x>0)的图象上(如图所示),0为坐标原点,AB∥x轴,则△OAB的面积为$\frac{5}{2}$.
点A在函数y=-$\frac{2}{x}$(x<0)的图象上,点B在y=$\frac{3}{x}$(x>0)的图象上(如图所示),0为坐标原点,AB∥x轴,则△OAB的面积为$\frac{5}{2}$.
分析 根据反比例函数系数k的几何意义即可得到结论.
解答 解:∵AB∥x轴,
∴△OAB的面积=$\frac{1}{2}$×|-2|+$\frac{1}{2}$×3=$\frac{5}{2}$.
故答案为:$\frac{5}{2}$.
点评 本题考查了反比例函数系数k的几何意义,反比例函数图象上点的坐标特征、图形与坐标的性质,三角形的面积公式,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
1.某艺术剧院门票价格如表所示:某团体准备了700元,全部用来购买指定日普通票和平日优惠票,且每种至少买一张.
门票价格一览表
(1)有多少种购票方案?列举所有可能结果;
(2)如果从上述方案中选中一种总票张数最少的情况,讲所购的票的票面朝下随意叠放在一起,随机抽两张,求正好抽出一张指定日普通票和一张平日优惠票的概率.
门票价格一览表
| 指定日普通票 | 200元 |
| 平日优惠票 | 100元 |
(2)如果从上述方案中选中一种总票张数最少的情况,讲所购的票的票面朝下随意叠放在一起,随机抽两张,求正好抽出一张指定日普通票和一张平日优惠票的概率.
11.在-(-$\frac{1}{2}$),|-$\frac{1}{2}$|,(-$\frac{1}{2}$)0,$\sqrt{\frac{1}{2}}$这四个数中,最大的数是( )
| A. | -(-$\frac{1}{2}$) | B. | |-$\frac{1}{2}$| | C. | (-$\frac{1}{2}$)0 | D. | $\sqrt{\frac{1}{2}}$ |
18.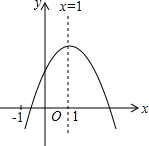 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列6个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤b2-4ac<0; ⑥a+b>m(am+b),(m≠1的实数)其中正确的结论有( )个.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列6个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤b2-4ac<0; ⑥a+b>m(am+b),(m≠1的实数)其中正确的结论有( )个.
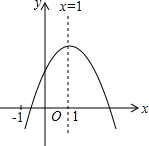 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列6个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤b2-4ac<0; ⑥a+b>m(am+b),(m≠1的实数)其中正确的结论有( )个.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列6个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤b2-4ac<0; ⑥a+b>m(am+b),(m≠1的实数)其中正确的结论有( )个.| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5 个 |
 如图,在△ABC中,以AC、BC分别向外作等边△ACF和等边△BCE,点P、M、N分别为AB、CF、CE的中点.
如图,在△ABC中,以AC、BC分别向外作等边△ACF和等边△BCE,点P、M、N分别为AB、CF、CE的中点.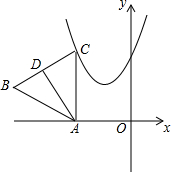 如图所示,在平面直角坐标系中,点A是x轴上一动点,过A作AC⊥x轴交抛物线y=x2+2x+2于点C,以AC为边作等边△ABC,高AD的最小值为$\frac{\sqrt{3}}{2}$.
如图所示,在平面直角坐标系中,点A是x轴上一动点,过A作AC⊥x轴交抛物线y=x2+2x+2于点C,以AC为边作等边△ABC,高AD的最小值为$\frac{\sqrt{3}}{2}$. 如图所示,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,OE交CD于点H,连接DE.
如图所示,平行四边形ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,OE交CD于点H,连接DE.