题目内容
17. 如图,在△ABC中,以AC、BC分别向外作等边△ACF和等边△BCE,点P、M、N分别为AB、CF、CE的中点.
如图,在△ABC中,以AC、BC分别向外作等边△ACF和等边△BCE,点P、M、N分别为AB、CF、CE的中点.①求证:PM=PN;
②求证:∠MPN=60°.
分析 ①取AC中点G,BC中点H,连接MG、PG、PH、HN,只要证明△MGP≌△PHN即可.
②连接MN,只要证明△MCN≌△MGP即可.
解答 证明:①取AC中点G,BC中点H,连接MG、PG、PH、HN.
∵△ACF、△BCE都是等边三角形,
∴AC=AF=CF,∠CAF=∠ACF=60°,BC=CE=BE,∠CBE=∠BCE=60°,
∵CM=MF,CG=AG,
∴GM∥AF,GM=$\frac{1}{2}$AF,同理PH=$\frac{1}{2}$AC,PH∥AC,PG=$\frac{1}{2}$BC,PG∥AC,HN=$\frac{1}{2}$BE,HN∥BE,
∴GM=PH,PG=HN,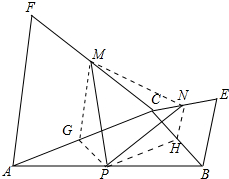
∴∠CGM=∠CAF=60°,∠CHN=∠CBE=60°,四边形CHPG是平行四边形,
∴∠CGP=∠CHP,∠CGM=∠CHN,
∴∠MGP=∠PHN,
在△MGP和△PHN中,
$\left\{\begin{array}{l}{MG=PH}\\{∠MGP=∠PHN}\\{PG=HN}\end{array}\right.$,
∴△MGP≌△PHN,
∴PM=PN.
②连接MN.
∵∠MCN=360°-∠ACF-∠BCE-∠ACB=360°-60°-60°-(180°-∠CGP)=60°+∠CGP=∠MGP,
在△MCN和△MGP中,
$\left\{\begin{array}{l}{CM=MG}\\{∠MGP=∠PHN}\\{PG=HN}\end{array}\right.$,
∴△MGP≌△PHN,
∴MN=PM=PN,
∴△PMN是等边三角形,
∴∠MPN=60°.
点评 本题考查全等三角形的判定和性质、等边三角形的性质、三角形中位线性质等知识,解题的关键是添加辅助线,构造全等三角形,熟练掌握三角形中位线性质也是解题关键,属于中考常考题型.

| 分数段 | 90<x≤100 | 80<x≤90 | 70<x≤80 | 60<x≤70 | 0≤x≤60 |
| 人数 | 100 | 200 | 80 | 80 | 40 |
②若用扇形统计图表示统计结果,则分数段为90<x≤100的人数所对应扇形的圆心角的度数为72°;
(2)试估算抽取学生地理会考模拟测试的平均成绩.

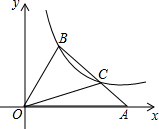 如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,且tan∠BAO=$\frac{1}{2}$,OC是△OAB的中线,点B在第一象限,且其纵坐标为3,点B,C在反比例函数y=$\frac{k}{x}$(x>0)的图象上.
如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,且tan∠BAO=$\frac{1}{2}$,OC是△OAB的中线,点B在第一象限,且其纵坐标为3,点B,C在反比例函数y=$\frac{k}{x}$(x>0)的图象上. 如图,D是AC上一点,DE∥AB,∠B=∠DAE,AD=AB,求证:AC=DE.
如图,D是AC上一点,DE∥AB,∠B=∠DAE,AD=AB,求证:AC=DE. 点A在函数y=-$\frac{2}{x}$(x<0)的图象上,点B在y=$\frac{3}{x}$(x>0)的图象上(如图所示),0为坐标原点,AB∥x轴,则△OAB的面积为$\frac{5}{2}$.
点A在函数y=-$\frac{2}{x}$(x<0)的图象上,点B在y=$\frac{3}{x}$(x>0)的图象上(如图所示),0为坐标原点,AB∥x轴,则△OAB的面积为$\frac{5}{2}$.