题目内容
18.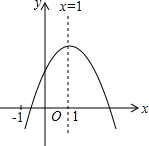 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列6个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤b2-4ac<0; ⑥a+b>m(am+b),(m≠1的实数)其中正确的结论有( )个.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列6个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤b2-4ac<0; ⑥a+b>m(am+b),(m≠1的实数)其中正确的结论有( )个.| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5 个 |
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:①∵该抛物线开口方向向下,
∴a<0.
∵抛物线对称轴方程x=-$\frac{b}{2a}$>0,
∴$\frac{b}{2a}$<0,
∴a、b异号,
∴b>0;
∵抛物线与y轴交与正半轴,
∴c>0,
∴abc<0;故①错误;
②∵当x=-1时,y<0,
∴a-b+c<0,
∴b>a+c,故②错误;
③根据抛物线的对称性知,当x=2时,y>0,即4a+2b+c>0;故③正确;
∵对称轴方程x=-$\frac{b}{2a}$=1,
∴b=-2a,
∴$\frac{b}{2}$=-a,
④根据抛物线的对称性知,当x=3时,y<0,即9a+3b+c<0,
∴9a+3b+c=-$\frac{3}{2}$b+c<0,
∴2c<3b.故④正确;
⑤∵抛物线与x轴有两个不同的交点,
∴b2-4ac>0.故⑤错误;
⑥x=m对应的函数值为y=am2+bm+c,
x=1对应的函数值为y=a+b+c,又x=1时函数取得最大值,
∴a+b+c>am2+bm+c,即a+b>am2+bm=m(am+b),
故⑥正确.
综上所述,正确的有3个.
故选B.
点评 主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
10.净水机的核心部件就是水处理反渗透膜,水处理反渗透膜就像是一个筛子,它的孔径只有0.11纳米,水在压力的作用下一层层过滤,离子以上的杂质像抗生素、重金属、细菌等都能过滤掉,0.11纳米即0.00000000011米,将0.11纳米用科学记数法表示为( )
| A. | 1.1×10-9米 | B. | 1.1×10-10米 | C. | 11×10-9米 | D. | 0.11×10-9米 |
7.已知抛物线y=-(x-1)2+m(m是常数),点A(x1,y1),B(x2,y2)在抛物线上,若x1<1<x2,x1+x2>2,则下列大小比较正确的是( )
| A. | m>y1>y2 | B. | m>y2>y1 | C. | y1>y2>m | D. | y2>y1>m |
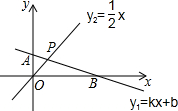 如图所示,已知直线y1=kx+b经过点(0,2),(-2,3),且与坐标轴交于点A、B两点.试:
如图所示,已知直线y1=kx+b经过点(0,2),(-2,3),且与坐标轴交于点A、B两点.试: 点A在函数y=-$\frac{2}{x}$(x<0)的图象上,点B在y=$\frac{3}{x}$(x>0)的图象上(如图所示),0为坐标原点,AB∥x轴,则△OAB的面积为$\frac{5}{2}$.
点A在函数y=-$\frac{2}{x}$(x<0)的图象上,点B在y=$\frac{3}{x}$(x>0)的图象上(如图所示),0为坐标原点,AB∥x轴,则△OAB的面积为$\frac{5}{2}$. 如图,在等腰直角三角形ABC中,∠A=90°,AB=AC=2,O为BC的中点,以O为圆心的圆弧分别与AB,AC相切于点D,E,则图中AD,AE与$\widehat{DE}$所围成的封闭图形的面积为1-$\frac{π}{4}$.
如图,在等腰直角三角形ABC中,∠A=90°,AB=AC=2,O为BC的中点,以O为圆心的圆弧分别与AB,AC相切于点D,E,则图中AD,AE与$\widehat{DE}$所围成的封闭图形的面积为1-$\frac{π}{4}$.