题目内容
14.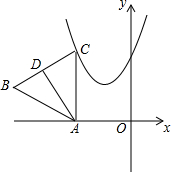 如图所示,在平面直角坐标系中,点A是x轴上一动点,过A作AC⊥x轴交抛物线y=x2+2x+2于点C,以AC为边作等边△ABC,高AD的最小值为$\frac{\sqrt{3}}{2}$.
如图所示,在平面直角坐标系中,点A是x轴上一动点,过A作AC⊥x轴交抛物线y=x2+2x+2于点C,以AC为边作等边△ABC,高AD的最小值为$\frac{\sqrt{3}}{2}$.
分析 先利用配方法得到抛物线的顶点坐标为(-1,1),再根据等边三角形的性质得AD=$\frac{\sqrt{3}}{2}$AC,由于AC的长等于点A的纵坐标,所以当点A在抛物线的顶点时,点A到x轴的距离最小,最小值为1,从而得到AD的最小值.
解答 解:∵y=x2+2x+2=(x+1)2+1,
∴抛物线的顶点坐标为(-1,1),
∵△ABC为等边三角形,
∴AD=$\frac{\sqrt{3}}{2}$AC,
∴当AC最短时,AD最小,
而AC⊥x轴,
∴AC的长等于点A的纵坐标,
当点A在抛物线的顶点时,点A到x轴的距离最小,最小值为1,
∴AD的最小值为$\frac{\sqrt{3}}{2}$.
故答案为$\frac{\sqrt{3}}{2}$.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了等边三角形的性质.

练习册系列答案
相关题目
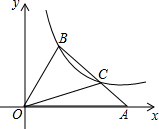 如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,且tan∠BAO=$\frac{1}{2}$,OC是△OAB的中线,点B在第一象限,且其纵坐标为3,点B,C在反比例函数y=$\frac{k}{x}$(x>0)的图象上.
如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴正半轴上,且tan∠BAO=$\frac{1}{2}$,OC是△OAB的中线,点B在第一象限,且其纵坐标为3,点B,C在反比例函数y=$\frac{k}{x}$(x>0)的图象上.
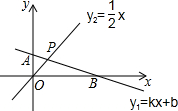 如图所示,已知直线y1=kx+b经过点(0,2),(-2,3),且与坐标轴交于点A、B两点.试:
如图所示,已知直线y1=kx+b经过点(0,2),(-2,3),且与坐标轴交于点A、B两点.试: 点A在函数y=-$\frac{2}{x}$(x<0)的图象上,点B在y=$\frac{3}{x}$(x>0)的图象上(如图所示),0为坐标原点,AB∥x轴,则△OAB的面积为$\frac{5}{2}$.
点A在函数y=-$\frac{2}{x}$(x<0)的图象上,点B在y=$\frac{3}{x}$(x>0)的图象上(如图所示),0为坐标原点,AB∥x轴,则△OAB的面积为$\frac{5}{2}$.