题目内容
14.已知关于x的方程x2+ax+b+1=0的解为x1=x2=2,则a+b的值为( )| A. | -3 | B. | -1 | C. | 1 | D. | 7 |
分析 由根与系数的关系可知:x1+x2=-a=-4,x1x2=b+1=4,进一步求得a、b即可.
解答 解:∵x1=x2=2都是方程x2+ax+b+1=0的根,
∴x1+x2=-a=4,x1x2=b+1=4,
∴a=-4,b=3,
∴a+b=-1
故选B.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$.

练习册系列答案
相关题目
2.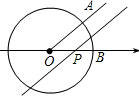 如图,已知⊙O圆心是数轴原点,半径为1,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是( )
如图,已知⊙O圆心是数轴原点,半径为1,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是( )
 如图,已知⊙O圆心是数轴原点,半径为1,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是( )
如图,已知⊙O圆心是数轴原点,半径为1,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是( )| A. | -1≤x≤1 | B. | -$\sqrt{2}$≤x≤$\sqrt{2}$ | C. | 0≤x≤$\sqrt{2}$ | D. | x>$\sqrt{2}$ |
 如图,点P为△ABC的边AB上的一点,连结PC,若∠1=∠B.
如图,点P为△ABC的边AB上的一点,连结PC,若∠1=∠B.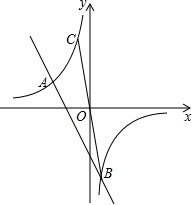 如图,在平面直角坐标系xOy中,一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于点A(-3,2)和点B(1,m),连接BO并延长与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于点C.
如图,在平面直角坐标系xOy中,一次函数y=k1x+b与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于点A(-3,2)和点B(1,m),连接BO并延长与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于点C.
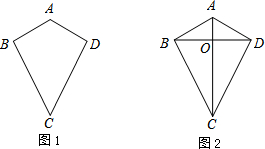
 已知:如图,△ABC是等边三角形,与BC平行的直线分别交AB和AC于点D,E,求证:△ADE是等边三角形.
已知:如图,△ABC是等边三角形,与BC平行的直线分别交AB和AC于点D,E,求证:△ADE是等边三角形.