题目内容
2.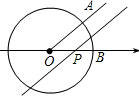 如图,已知⊙O圆心是数轴原点,半径为1,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是( )
如图,已知⊙O圆心是数轴原点,半径为1,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是( )| A. | -1≤x≤1 | B. | -$\sqrt{2}$≤x≤$\sqrt{2}$ | C. | 0≤x≤$\sqrt{2}$ | D. | x>$\sqrt{2}$ |
分析 首先作出圆的切线,求出直线与圆相切时的P的取值,再结合图象可得出P的取值范围,即可得出答案.
解答  解:∵半径为1的圆,∠AOB=45°,过点P且与OA平行的直线与⊙O有公共点,
解:∵半径为1的圆,∠AOB=45°,过点P且与OA平行的直线与⊙O有公共点,
∴当P′C与圆相切时,切点为C,
∴OC⊥P′C,
CO=1,∠P′OC=45°,OP′=$\sqrt{2}$,
∴过点P且与OA平行的直线与⊙O有公共点,即0≤x≤$\sqrt{2}$,
同理点P在点O左侧时,0$≤x≤\sqrt{2}$
∴0≤x≤$\sqrt{2}$.
故选C.
点评 此题主要考查了直线与圆的位置关系,作出切线找出直线与圆有交点的分界点是解决问题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
12.一元一次不等式-x-2<1-2x的正整数解有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 无数个 |
17.下列各式:$\frac{1}{8}(1-x)$,$\frac{4x}{π-3}$,$\frac{{{x^2}-{y^2}}}{2}$,$\frac{1}{x}+x$,$\frac{{5{x^2}}}{x}$,其中分式共有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
14.已知关于x的方程x2+ax+b+1=0的解为x1=x2=2,则a+b的值为( )
| A. | -3 | B. | -1 | C. | 1 | D. | 7 |
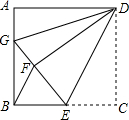 如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出以下结论:①△DAG≌△DFG;②BG=2AG;③S△DGF=120;④S△BEF=$\frac{72}{5}$.其中所有正确结论的个数是( )
如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出以下结论:①△DAG≌△DFG;②BG=2AG;③S△DGF=120;④S△BEF=$\frac{72}{5}$.其中所有正确结论的个数是( ) 如图,已知∠BAD=∠CAD,如果把∠BAD沿着AD翻折过来,射线AB与射线AC将会有怎样的位置关系?如果线段AB的长与线段AC的长相等,这时点B与点C有怎样的位置关系?
如图,已知∠BAD=∠CAD,如果把∠BAD沿着AD翻折过来,射线AB与射线AC将会有怎样的位置关系?如果线段AB的长与线段AC的长相等,这时点B与点C有怎样的位置关系?