题目内容
9.如图1,在四边形ABCD中,BA=BC,∠ABC=60°,∠ADC=30°,连接对角线BD.(1)将线段CD绕点C顺时针旋转60°得到线段CE,连接AE.
①依题意补全图1;
②试判断AE与BD的数量关系,并证明你的结论;
(2)在(1)的条件下,直接写出线段DA、DB和DC之间的数量关系;
(3)如图2,F是对角线BD上一点,且满足∠AFC=150°,连接FA和FC,探究线段FA、FB和FC之间的数量关系,并证明.

分析 (1)①根据题意画图即可;
②连接AC,证明△BCD≌△ACE即可;
(2)连接DE,可证三角形ADE为直角三角形,由勾股定理即可得出结论;
(3)将线段CF绕点C顺时针旋转60°得到线段CE,连接EF,EA,证明△BCF≌△ACE和直角三角形AEF,结合勾股定理即可证明.
解答 解:(1)①补全图形如图1,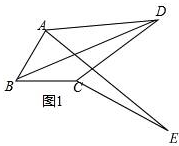
②判断AE=BD,
证明:如图2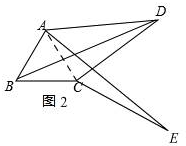
连接AC,
∵BA=BC,∠ABC=60°,
∴△ABC是等边三角形,
∴∠ACB=60°,CA=CB,
∵将线段CD绕点C顺时针旋转60°得到线段CE,
∴CD=CE,∠DCE=60°,
∴∠BCD=∠ACE,
在△BCD和△ACE中,
$\left\{\begin{array}{l}{CB=CA}\\{∠BCD=∠ACE}\\{CD=CE}\end{array}\right.$,
∴△BCD≌△ACE,
∴BD=AE;
(2)结论:DA2+DC2=DB2;
(3)结论:FA2+FC2=FB2或BF2=AF2+CF2+$\sqrt{3}$AF•CF.
证明:①如图3,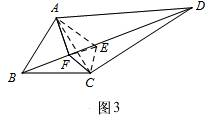
连接AC,
∵BA=BC,∠ABC=60°,
∴△ABC是等边三角形,
∴∠ACB=60°,CA=CB,
将线段CF绕点C顺时针旋转60°得到线段CE,连接EF,EA,
∴CE=CF,∠FCE=60°,
∴△CEF是等边三角形,
∴∠CFE=60°,FE=FC,
∴∠BCF=∠ACE,
在△BCF和△ACE中,
$\left\{\begin{array}{l}{CB=CA}\\{∠BCF=∠ACE}\\{CF=CE}\end{array}\right.$,
∴△BCF≌△ACE,
∴FB=AE,
∵∠AFC=150°,∠CFE=60°,
∴∠AFE=90°,
在Rt△AEF中,FA2+FE2=AE2,
∴FA2+FC2=FB2.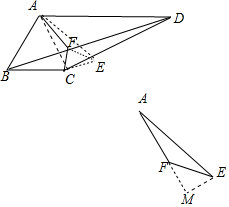
②如图当∠AFC=150°,作等边三角形FCE,连接AC、AE.
同理可证△BCF≌△ACE,BF=AE.
∵∠CFE=60°,
∴∠AFE=360°-150°-60°150°,
作EM⊥AF于M.(下图),
在Rt△EFM中,∵∠EFM=30°,
∴EM=$\frac{1}{2}$EF,FM=$\frac{\sqrt{3}}{2}$EF,
在Rt△AME中,AE2=AM2+EM2,
∴AE2=(AF+$\frac{\sqrt{3}}{2}$EF)2+($\frac{1}{2}$EF)2,
∴AE2=AF2+EF2+$\sqrt{3}$AF•EF,
∵AE=BF,EF=CF,
∴BF2=AF2+CF2+$\sqrt{3}$AF•CF.
点评 此题主要考查几何变换综合问题,熟悉旋转的性质,会在旋转变换中确定全等三角形并会构造直角三角形运用勾股定理是解题的关键.

 字词句段篇系列答案
字词句段篇系列答案 为了解今年全县2000名初中学生“创新能力”大赛的笔试情况,随机抽取了部分同学的成绩,整理并制作如图所示图表,请你根据图表中信息,解答下列问题?
为了解今年全县2000名初中学生“创新能力”大赛的笔试情况,随机抽取了部分同学的成绩,整理并制作如图所示图表,请你根据图表中信息,解答下列问题?| 分数段 | 步数 | 频率 |
| 60≤x<70 | 30 | 0.1 |
| 70≤x<80 | 90 | n |
| 80≤x<90 | m | 0.4 |
| 90≤x<100 | 60 | 0.2 |
(2)在表中m=120; m=0.3;
(3)补全频数分布直方图.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
| A. | -3 | B. | -1 | C. | 1 | D. | 7 |
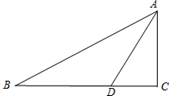 如图,已知在Rt△ABC中,∠C=90°,AD是∠BAC的角分线.
如图,已知在Rt△ABC中,∠C=90°,AD是∠BAC的角分线.
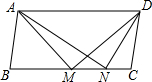 如图,平行四边形ABCD中,M、N是BC边上的点,且∠AMD=∠AND=90°,则下列结论中一定成立的是(1)(3)(4)(把所有正确结论的序号都填在横线上)
如图,平行四边形ABCD中,M、N是BC边上的点,且∠AMD=∠AND=90°,则下列结论中一定成立的是(1)(3)(4)(把所有正确结论的序号都填在横线上)