题目内容
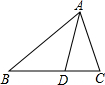 在△ABC中,点D在BC上,BD=AD=AC,∠CAD=28°,求∠BAC的度数.
在△ABC中,点D在BC上,BD=AD=AC,∠CAD=28°,求∠BAC的度数.考点:等腰三角形的性质
专题:
分析:根据等腰三角形两底角相等可得∠B=∠BAD,∠ADC=∠C,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BAD,然后根据∠BAC=∠BAD+∠CAD计算即可得解.
解答:解:∵BD=AD=AC,∠CAD=28°,
∴∠B=∠BAD,∠ADC=∠C=
(180°-28°)=76°.
又∵∠ADC=∠B+∠BAD=2∠B,
∴∠C=2∠B,
∴∠B=∠BAD=
×76°=38°,
∴∠BAC=∠BAD+∠CAD=38°+28°=66°.
∴∠B=∠BAD,∠ADC=∠C=
| 1 |
| 2 |
又∵∠ADC=∠B+∠BAD=2∠B,
∴∠C=2∠B,
∴∠B=∠BAD=
| 1 |
| 2 |
∴∠BAC=∠BAD+∠CAD=38°+28°=66°.
点评:本题考查了等腰三角形的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
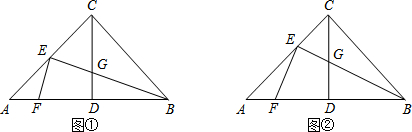
 如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<12),连接DE,当△BDE是直角三角形时,t的值为
如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<12),连接DE,当△BDE是直角三角形时,t的值为 DE为△ABC的中位线,连接BE,且BE=BC,延长DE到点F,使EF=BE,连接CF,BF.
DE为△ABC的中位线,连接BE,且BE=BC,延长DE到点F,使EF=BE,连接CF,BF.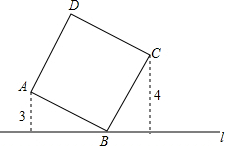 如图,直线l过正方形ABCD的顶点B,点A、点C到直线l的距离分别是3和4,则该正方形的边长是
如图,直线l过正方形ABCD的顶点B,点A、点C到直线l的距离分别是3和4,则该正方形的边长是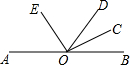 如图,AB是一条直线,OD是一条射线,OV,OE分别是∠BOD,∠AOD的平分线,∠BOC=15°48′.
如图,AB是一条直线,OD是一条射线,OV,OE分别是∠BOD,∠AOD的平分线,∠BOC=15°48′.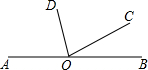 如图,∠BOC与∠AOC互为补角,OD平分∠AOC,∠BOC=n°,则∠DOB=
如图,∠BOC与∠AOC互为补角,OD平分∠AOC,∠BOC=n°,则∠DOB=