题目内容
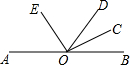 如图,AB是一条直线,OD是一条射线,OV,OE分别是∠BOD,∠AOD的平分线,∠BOC=15°48′.
如图,AB是一条直线,OD是一条射线,OV,OE分别是∠BOD,∠AOD的平分线,∠BOC=15°48′.(1)求∠AOE的度数
(2)图中有没有与∠EOD互余的角?若有,请写出来
(3)图中有没有与∠EOB互补的角?若有,请写出来.
考点:余角和补角
专题:
分析:(1)先求出∠BOD=2∠BOC=31°36′,再求出∠AOD=180°-∠BOD=148°24′,即可求出∠AOE=74°12′;
(2)求出∠EOD+∠DOC=∠EOD+∠BOC=
×180°=90°,即可得出结论;
(3)求出∠AOE+∠EOB=∠EOD+∠EOB=180°,即可得出结论.
(2)求出∠EOD+∠DOC=∠EOD+∠BOC=
| 1 |
| 2 |
(3)求出∠AOE+∠EOB=∠EOD+∠EOB=180°,即可得出结论.
解答:解:(1)∵∠BOC=15°48′,OC平分∠BOD,
∴∠BOD=2∠BOC=31°36′,
∴∠AOD=180°-∠BOD=148°24′,
∵OE平分∠AOD,
∴∠AOE=
∠AOD=74°12′;
(2)有;∵OC、OE分别是∠BOD、∠AOD的平分线,
∴∠BOC=∠DOC=
∠BOD,∠AOE=∠EOD=
∠AOD,
∵∠BOD+∠AOD=180°,
∴∠EOD+∠DOC=∠EOD+∠BOC=
×180°=90°,
∴图中与∠EOD互余的角为∠DOC,∠BOC;
(3)有;∠AOE+∠EOB=∠EOD+∠EOB=180°,
∴图中与∠EOB互补的角为∠AOE,∠EOD.
∴∠BOD=2∠BOC=31°36′,
∴∠AOD=180°-∠BOD=148°24′,
∵OE平分∠AOD,
∴∠AOE=
| 1 |
| 2 |
(2)有;∵OC、OE分别是∠BOD、∠AOD的平分线,
∴∠BOC=∠DOC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠BOD+∠AOD=180°,
∴∠EOD+∠DOC=∠EOD+∠BOC=
| 1 |
| 2 |
∴图中与∠EOD互余的角为∠DOC,∠BOC;
(3)有;∠AOE+∠EOB=∠EOD+∠EOB=180°,
∴图中与∠EOB互补的角为∠AOE,∠EOD.
点评:本题考查了余角和补角以及角平分线的定义;弄清各个角之间的关系是解决问题的关键.

练习册系列答案
相关题目
已知
=
,则( )
| a |
| b |
| 2 |
| 3 |
| A、2a=3b | ||||
B、
| ||||
C、
| ||||
D、
|




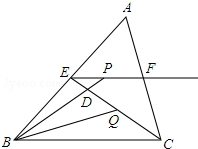 如图所示,在△ABC中,E、F分别是AB、AC的中点,BC=6,CE=5,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于Q,当EP+BP=18时,则CQ的值为
如图所示,在△ABC中,E、F分别是AB、AC的中点,BC=6,CE=5,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于Q,当EP+BP=18时,则CQ的值为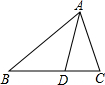 在△ABC中,点D在BC上,BD=AD=AC,∠CAD=28°,求∠BAC的度数.
在△ABC中,点D在BC上,BD=AD=AC,∠CAD=28°,求∠BAC的度数.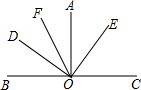 如图所示,∠AOB=∠AOC=90°,∠DOE=90°,OF平分∠AOD,∠AOE=36°.
如图所示,∠AOB=∠AOC=90°,∠DOE=90°,OF平分∠AOD,∠AOE=36°.
 如图,在△ABC中,∠ABC=∠C,BD平分∠ABC,∠A=36°,则∠BDC=
如图,在△ABC中,∠ABC=∠C,BD平分∠ABC,∠A=36°,则∠BDC=