题目内容
如图,∠ACB=90°,CD⊥AB,垂足为D,点E在AC上,BE交CD于点G,EF⊥BE交AB于点F.
(1)如图①,若AC=BC,CE=EA,探索线段EF与EG的数量关系,并证明你的结论;
(2)如图②,若AC=mBC,CE=kEA,探索线段EF与EG的数量关系,并证明你的结论.
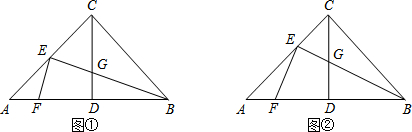
(1)如图①,若AC=BC,CE=EA,探索线段EF与EG的数量关系,并证明你的结论;
(2)如图②,若AC=mBC,CE=kEA,探索线段EF与EG的数量关系,并证明你的结论.

考点:相似三角形的判定与性质
专题:
分析:(1)作EH⊥CD,EQ⊥AB,利用AAS先证△AEQ≌△ECH,易得EQ=EH,把EQ=EH作为一个条件,再利用ASA易证Rt△EFQ≌Rt△EGH,从而有EF=EG;
(2)过点E作EQ⊥AB,EH⊥CD,根据CD⊥AB和EF⊥BE先证明△EFQ与△EGH相似,得到EF:EG=EQ:EH,再根据平行线分线段成比例定理求出EQ:CG=AE:AC,EH:AD=CE:AC,结合CE=kEA即可用CD、AD表示出EQ与EH,再利用∠A的正切值即可求出.
(2)过点E作EQ⊥AB,EH⊥CD,根据CD⊥AB和EF⊥BE先证明△EFQ与△EGH相似,得到EF:EG=EQ:EH,再根据平行线分线段成比例定理求出EQ:CG=AE:AC,EH:AD=CE:AC,结合CE=kEA即可用CD、AD表示出EQ与EH,再利用∠A的正切值即可求出.
解答: 证明:(1)作EH⊥CD,EQ⊥AB,
证明:(1)作EH⊥CD,EQ⊥AB,
∵AC=BC,CD⊥AB,∠ACB=90°,
∴∠ADC=90°,∠A=∠ACD=45°,
∵EH⊥CD,EQ⊥AB,
∴∠AQE=∠EHC=90°,
在△AEQ与△ECH中,
,
∴△AEQ≌△ECH(AAS),
∴EQ=EH,
∵EH⊥CD,EQ⊥AB,CD⊥AB,
∴四边形EQDH是矩形,
∴∠QEH=90°,
∴∠FEQ=∠GEH=90°-∠QEB,
又∵∠EQF=∠EHG=90°,EQ=EH,
∴Rt△EFQ≌Rt△EGH,
∴EF=EG;
(2)过E作EQ⊥AB,EH⊥CD,
∵CD⊥AB,
∴EQ∥CD,EH∥AB,
∵EF⊥BE,
∴∠EFQ+∠EBF=90°,
∵∠EBF+∠DGB=90°,∠DGB=∠EGH(对顶角相等)
∴∠EFQ=∠EGH,
∴△EFQ∽△EGH,
∴
=
,
在△ADC中,
∵EQ∥CD,
∴
=
,
又∵CE=kEA,
∴AC=(k+1)AE
∴CD=(k+1)EQ,
同理
=
,
∴AD=
EH,
∵∠ACB=90°,CD⊥AB,AC=mBC
tanA=
=
=
,
即
=
,
∴
=
,
∴EF=
EG.
 证明:(1)作EH⊥CD,EQ⊥AB,
证明:(1)作EH⊥CD,EQ⊥AB,∵AC=BC,CD⊥AB,∠ACB=90°,
∴∠ADC=90°,∠A=∠ACD=45°,
∵EH⊥CD,EQ⊥AB,
∴∠AQE=∠EHC=90°,
在△AEQ与△ECH中,
|
∴△AEQ≌△ECH(AAS),
∴EQ=EH,
∵EH⊥CD,EQ⊥AB,CD⊥AB,
∴四边形EQDH是矩形,
∴∠QEH=90°,
∴∠FEQ=∠GEH=90°-∠QEB,
又∵∠EQF=∠EHG=90°,EQ=EH,
∴Rt△EFQ≌Rt△EGH,
∴EF=EG;
(2)过E作EQ⊥AB,EH⊥CD,
∵CD⊥AB,
∴EQ∥CD,EH∥AB,
∵EF⊥BE,
∴∠EFQ+∠EBF=90°,
∵∠EBF+∠DGB=90°,∠DGB=∠EGH(对顶角相等)
∴∠EFQ=∠EGH,
∴△EFQ∽△EGH,
∴
| EF |
| EG |
| EQ |
| EH |
在△ADC中,
∵EQ∥CD,
∴
| EQ |
| CD |
| AE |
| AC |
又∵CE=kEA,
∴AC=(k+1)AE
∴CD=(k+1)EQ,
同理
| EH |
| AD |
| CE |
| AC |
∴AD=
| k+1 |
| k |
∵∠ACB=90°,CD⊥AB,AC=mBC
tanA=
| CD |
| AD |
| BC |
| AC |
| 1 |
| m |
即
| (k+1)EQ | ||
|
| 1 |
| m |
∴
| EQ |
| EH |
| 1 |
| km |
∴EF=
| 1 |
| km |
点评:考查了相似三角形的判定与性质,本题难度较大,主要利用相似三角形对应边成比例求解,正确作出辅助线是解本题的关键,这就要求同学们在平时的学习中不断积累经验,开拓视野.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知
=
,则( )
| a |
| b |
| 2 |
| 3 |
| A、2a=3b | ||||
B、
| ||||
C、
| ||||
D、
|





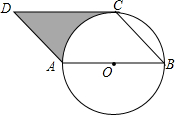 如图,已知在?ABCD中,AB=4,∠DAB=135°,以AB为直径的⊙O恰好经过点C.
如图,已知在?ABCD中,AB=4,∠DAB=135°,以AB为直径的⊙O恰好经过点C. 如图,在半径为2,圆心角为90°的扇形ACB内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为
如图,在半径为2,圆心角为90°的扇形ACB内,以BC为直径作半圆,交弦AB于点D,连接CD,则阴影部分的面积为 如图所示,ABCD是正方形,AE∥DB,BE=BD,BE交AD于F,试说明:△DEF是等腰三角形.
如图所示,ABCD是正方形,AE∥DB,BE=BD,BE交AD于F,试说明:△DEF是等腰三角形.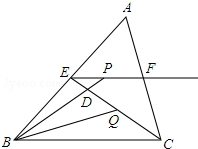 如图所示,在△ABC中,E、F分别是AB、AC的中点,BC=6,CE=5,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于Q,当EP+BP=18时,则CQ的值为
如图所示,在△ABC中,E、F分别是AB、AC的中点,BC=6,CE=5,动点P在射线EF上,BP交CE于D,∠CBP的平分线交CE于Q,当EP+BP=18时,则CQ的值为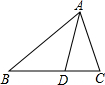 在△ABC中,点D在BC上,BD=AD=AC,∠CAD=28°,求∠BAC的度数.
在△ABC中,点D在BC上,BD=AD=AC,∠CAD=28°,求∠BAC的度数.