题目内容
在圆中,一条弧所对的圆周角为40度,则这条弧所对的圆心角等于 度.
考点:圆周角定理
专题:
分析:根据圆周角定理(在同圆中,圆周角等于它所夹弧所对的圆心角的一半)求出即可.
解答:解:根据圆周角定理得:在圆中,一条弧所对的圆周角为40度,则这条弧所对的圆心角为2×40°=80°.
故答案为:80.
故答案为:80.
点评:本题考查了圆周角定理的应用,能正确运用圆周角定理进行推理是解此题的关键,注意:在同圆中,圆周角等于它所夹弧所对的圆心角的一半.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知
=
,则( )
| a |
| b |
| 2 |
| 3 |
| A、2a=3b | ||||
B、
| ||||
C、
| ||||
D、
|
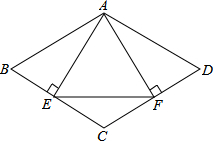 如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则的△AEF的面积是( )
如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则的△AEF的面积是( )A、4
| ||
B、3
| ||
C、2
| ||
D、
|
将不等式组
的解集表示在数轴上,正确的是( )
|
A、 |
B、 |
C、 |
D、 |
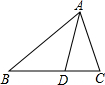 在△ABC中,点D在BC上,BD=AD=AC,∠CAD=28°,求∠BAC的度数.
在△ABC中,点D在BC上,BD=AD=AC,∠CAD=28°,求∠BAC的度数.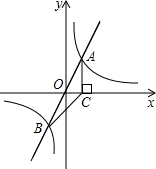 如图,在平面直角坐标系xOy中,正比例函数y=2x与反比例函数y=
如图,在平面直角坐标系xOy中,正比例函数y=2x与反比例函数y= 如图,在⊙O中,将△OAB绕点O顺时针方向旋转85°,得到△OCD.若∠BAC=15°,则∠BOC的度数为
如图,在⊙O中,将△OAB绕点O顺时针方向旋转85°,得到△OCD.若∠BAC=15°,则∠BOC的度数为 如图,在△ABC中,∠ABC=∠C,BD平分∠ABC,∠A=36°,则∠BDC=
如图,在△ABC中,∠ABC=∠C,BD平分∠ABC,∠A=36°,则∠BDC=



