题目内容
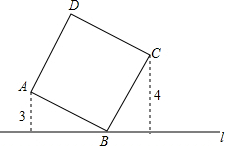 如图,直线l过正方形ABCD的顶点B,点A、点C到直线l的距离分别是3和4,则该正方形的边长是
如图,直线l过正方形ABCD的顶点B,点A、点C到直线l的距离分别是3和4,则该正方形的边长是考点:全等三角形的判定与性质,勾股定理,正方形的性质
专题:
分析:由正方形的性质可以得出∠ABC=90°,AB=BC,就有∠ABE+∠CBF=90°,进而得出∠ABE=∠BCF,就有△ABE≌△BCF,AE=BF,由勾股定理就可以求出结论.
解答:解:∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC,
∴∠ABE+∠CBF=90°.
∵∠AEB=∠CFB=90°,
∴∠CBF+∠BCF=90°,
∴∠ABE=∠BCF.
在△ABE和△BCF中,
,
∴Rt△ABE≌Rt△BCF(AAS),
∴AE=BF.
∵AE=3,
∴BF=3.
在At△BFC中,由勾股定理,得
BC=5,
∴正方形的边长是5.
故答案为:5.
∴∠ABC=90°,AB=BC,

∴∠ABE+∠CBF=90°.
∵∠AEB=∠CFB=90°,
∴∠CBF+∠BCF=90°,
∴∠ABE=∠BCF.
在△ABE和△BCF中,
|
∴Rt△ABE≌Rt△BCF(AAS),
∴AE=BF.
∵AE=3,
∴BF=3.
在At△BFC中,由勾股定理,得
BC=5,
∴正方形的边长是5.
故答案为:5.
点评:本题考查了正方形的性质的运用,直角三角形的性质的运用,全等三角形的判定及性质的运用,勾股定理的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
解为x=0的方程是( )
| A、2x-6=0 | ||||||
| B、3(x-2)-2(x-3)=5x | ||||||
C、
| ||||||
D、
|

 如图所示,ABCD是正方形,AE∥DB,BE=BD,BE交AD于F,试说明:△DEF是等腰三角形.
如图所示,ABCD是正方形,AE∥DB,BE=BD,BE交AD于F,试说明:△DEF是等腰三角形.

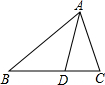 在△ABC中,点D在BC上,BD=AD=AC,∠CAD=28°,求∠BAC的度数.
在△ABC中,点D在BC上,BD=AD=AC,∠CAD=28°,求∠BAC的度数.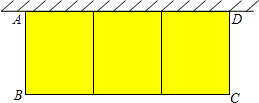 如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米.
如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米.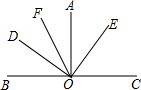 如图所示,∠AOB=∠AOC=90°,∠DOE=90°,OF平分∠AOD,∠AOE=36°.
如图所示,∠AOB=∠AOC=90°,∠DOE=90°,OF平分∠AOD,∠AOE=36°. 如图,在⊙O中,将△OAB绕点O顺时针方向旋转85°,得到△OCD.若∠BAC=15°,则∠BOC的度数为
如图,在⊙O中,将△OAB绕点O顺时针方向旋转85°,得到△OCD.若∠BAC=15°,则∠BOC的度数为