题目内容
2.(1)化简求值:($\frac{a}{a-b}$-$\frac{{a}^{2}}{{a}^{2}-2ab+{b}^{2}}$)÷($\frac{a}{a+b}$-$\frac{{a}^{2}}{{a}^{2}-{b}^{2}}$)+1,其中a=$\frac{2}{3}$,b=-3.(2)已知x为整数,且$\frac{2}{x+3}$+$\frac{2}{3-x}$+$\frac{2x+18}{{x}^{2}-9}$为负整数,y=$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$+$\frac{{x}^{2}-x}{x+1}$-$\frac{1}{x}$+1,把x与y代入(xy-x2)÷$\frac{{x}^{2}-2xy+{y}^{2}}{xy}$×$\frac{x-y}{{x}^{2}}$+xy求值.
分析 (1)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分后计算得到最简结果,把a与b的值代入计算即可求出值;
(2)根据负整数,可得x的值,根据自变量与函数值的对应关系,可得y的值,根据代数式求值,可得答案.
解答 解:(1)原式=[$\frac{a(a-b)}{(a-b)(a-b)}$-$\frac{{a}^{2}}{(a-b)^{2}}$]÷[$\frac{a(a-b)}{(a+b)(a-b)}$-$\frac{{a}^{2}}{(a+b)(a-b)}$]+1
=$\frac{-ab}{(a-b)^{2}}$÷$\frac{-ab}{(a+b)(a-b)}$+1
=$\frac{a+b}{a-b}$+1
=$\frac{2a}{a-b}$;
当a=$\frac{2}{3}$,b=-3时,原式=$\frac{2×\frac{2}{3}}{\frac{2}{3}-(-3)}$=$\frac{4}{11}$;
(2)由x为整数,$\frac{2}{x+3}$+$\frac{2}{3-x}$+$\frac{2x+18}{{x}^{2}-9}$=$\frac{2}{x-3}$为负整数,得
x=2,x=1(不符合题意,舍),
y=$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$+$\frac{{x}^{2}-x}{x+1}$-$\frac{1}{x}$+1=1,
(xy-x2)÷$\frac{{x}^{2}-2xy+{y}^{2}}{xy}$×$\frac{x-y}{{x}^{2}}$+xy
=x(y-x)×$\frac{xy}{(x-y)^{2}}$×$\frac{x-y}{{x}^{2}}$+xy
=-y+xy,
当x=2,y=1时,原式=-1+2×1=1.
点评 本题考查了分式的化简求值,利用x为整数$\frac{2}{x-3}$且x2-1≠0为负整数得出x的值是解题关键.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案| A. | 1 | B. | -1 | C. | 2017 | D. | -2017 |
| A. | x2-1+y2=(x-1)(x+1)+y2 | B. | x(a-b)=ax-bx | ||
| C. | ax+bx+c=x(a+b)+c | D. | x2-1=(x+1)(x-1) |
| A. | (2,3) | B. | (-2,3) | C. | (2,-3) | D. | (-2,-3) |
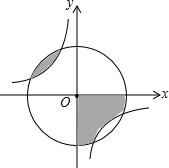 如图,反比例函数y=$\frac{k}{x}$(k<0)的图象与⊙O相交,某同学在⊙O内做随机扎针实验,针头落在阴影区域的概率是( )
如图,反比例函数y=$\frac{k}{x}$(k<0)的图象与⊙O相交,某同学在⊙O内做随机扎针实验,针头落在阴影区域的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | -$\frac{1}{k}$ | D. | $\frac{1}{π}$ |
 如图,将一副三角尺的直角顶点叠放在点C处,∠D=30°,∠B=45°,求:
如图,将一副三角尺的直角顶点叠放在点C处,∠D=30°,∠B=45°,求: