题目内容
7.下列各式从左到右的变形中,是因式分解的为( )| A. | x2-1+y2=(x-1)(x+1)+y2 | B. | x(a-b)=ax-bx | ||
| C. | ax+bx+c=x(a+b)+c | D. | x2-1=(x+1)(x-1) |
分析 将多项式化为几个整式的乘积形式成为多项式的因式分解.
解答 解:根据因式分解的意义可知:D正确
故选(D)
点评 本题考查因式分解的意义,属于基础题型.

练习册系列答案
相关题目
15.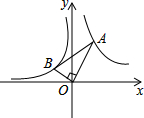 如图,已知第一象限内的点A在反比例函数y=$\frac{4}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,$\frac{OB}{OA}$=$\frac{3}{4}$,则k的值为( )
如图,已知第一象限内的点A在反比例函数y=$\frac{4}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,$\frac{OB}{OA}$=$\frac{3}{4}$,则k的值为( )
 如图,已知第一象限内的点A在反比例函数y=$\frac{4}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,$\frac{OB}{OA}$=$\frac{3}{4}$,则k的值为( )
如图,已知第一象限内的点A在反比例函数y=$\frac{4}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,$\frac{OB}{OA}$=$\frac{3}{4}$,则k的值为( )| A. | $\frac{9}{4}$ | B. | -$\frac{9}{4}$ | C. | -$\frac{3}{4}$ | D. | -3 |
12.下列方程是一元二次方程的是( )
| A. | x-2=0 | B. | x2-4x-1=0 | C. | x3-2x-3=0 | D. | xy+1=0 |
19.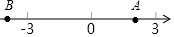 点A、B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b-a<0;乙:a+b>0;丙:|a|<|b|;丁:$\frac{b}{a}$>0,其中正确的是( )
点A、B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b-a<0;乙:a+b>0;丙:|a|<|b|;丁:$\frac{b}{a}$>0,其中正确的是( )
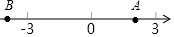 点A、B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b-a<0;乙:a+b>0;丙:|a|<|b|;丁:$\frac{b}{a}$>0,其中正确的是( )
点A、B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b-a<0;乙:a+b>0;丙:|a|<|b|;丁:$\frac{b}{a}$>0,其中正确的是( )| A. | 甲乙 | B. | 甲丙 | C. | 丙丁 | D. | 乙丁 |
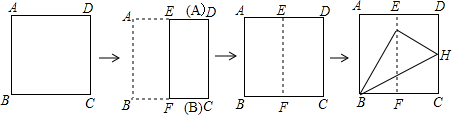
16.如图,先将一张长方形的纸沿虚线对折,再对折,然后按图中虚线剪下,将剪下的纸展开,一定可以得到一个( )


| A. | 菱形 | B. | 矩形 | C. | 正方形 | D. | 梯形 |
17.下列计算正确的是( )
| A. | x4+x4=2x8 | B. | (x2y)3=x6y | C. | -(x2)3=x5 | D. | -x3•(-x)5=x8 |
 如图,在正方形网格图中,若⊙O的半径为2,则阴影部分两个小扇形的面积之和为π.(结果保留π)
如图,在正方形网格图中,若⊙O的半径为2,则阴影部分两个小扇形的面积之和为π.(结果保留π)