题目内容
11. 如图,将一副三角尺的直角顶点叠放在点C处,∠D=30°,∠B=45°,求:
如图,将一副三角尺的直角顶点叠放在点C处,∠D=30°,∠B=45°,求:(1)若∠DCE=35°,求∠ACB的度数.
(2)若∠ACB=120°,求∠DCE的度数.
(3)猜想∠ACB和∠DCE的关系,并说明理由.
分析 (1))由∠ACD=∠BCE=90°,根据图形可知∠ACB=180°-∠DCE;
(2)由∠ACD=∠BCE=90°,根据图形可知∠DCE=180°-∠ACB;
(3)由∠ACD=∠BCE=90°,得出∠ACE+∠DCE+∠DCE+∠BCD=180°,即可证出∠ACB+∠DCE=180°.
解答 解:(1)∵∠ECB=90°,∠DCE=35°
∴∠DCB=90°-35°=55°
∵∠ACD=90°
∴∠ACB=∠ACD+∠DCB=145°.
(2)∵∠ACB=120°,∠ACD=90°
∴∠DCB=120°-90°=30°
∵∠ECB=90°
∴∠DCE=90°-30°=60°.
(3)猜想得∠ACB+∠DCE=180°(或∠ACB与∠DCE互补)
理由:∵∠ECB=90°,∠ACD=90°
∴∠ACB=∠ACD+∠DCB=90°+∠DCB
∠DCE=∠ECB-∠DCB=90°-∠DCB
∴∠ACB+∠DCE=180°.
点评 本题考查了余角和补角的定义;弄清两个角之间的互余和互补关系是解题的关键.

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
19.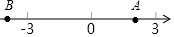 点A、B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b-a<0;乙:a+b>0;丙:|a|<|b|;丁:$\frac{b}{a}$>0,其中正确的是( )
点A、B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b-a<0;乙:a+b>0;丙:|a|<|b|;丁:$\frac{b}{a}$>0,其中正确的是( )
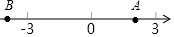 点A、B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b-a<0;乙:a+b>0;丙:|a|<|b|;丁:$\frac{b}{a}$>0,其中正确的是( )
点A、B在数轴上的位置如图所示,其对应的数分别是a和b,对于以下结论:甲:b-a<0;乙:a+b>0;丙:|a|<|b|;丁:$\frac{b}{a}$>0,其中正确的是( )| A. | 甲乙 | B. | 甲丙 | C. | 丙丁 | D. | 乙丁 |
6.-2017的相反数和倒数分别是( )
| A. | 2017,$\frac{1}{2017}$ | B. | $-\frac{1}{2017}$,2017 | C. | 2017,$-\frac{1}{2017}$ | D. | -2017,$\frac{1}{2017}$ |
16.如图,先将一张长方形的纸沿虚线对折,再对折,然后按图中虚线剪下,将剪下的纸展开,一定可以得到一个( )


| A. | 菱形 | B. | 矩形 | C. | 正方形 | D. | 梯形 |
20.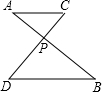 如图,线段AB与CD相交于点P,AC∥BD,∠A=39°,∠D=50°,则( )
如图,线段AB与CD相交于点P,AC∥BD,∠A=39°,∠D=50°,则( )
 如图,线段AB与CD相交于点P,AC∥BD,∠A=39°,∠D=50°,则( )
如图,线段AB与CD相交于点P,AC∥BD,∠A=39°,∠D=50°,则( )| A. | ∠APD=39° | B. | ∠APD=50° | C. | ∠APD=89° | D. | ∠APD=76° |
1.下面合并同类项正确的是( )
| A. | 3x+2x2=5x3 | B. | 2a2b-2a2b-a2b=1 | C. | -ab-ab=0 | D. | -xy2+xy2=0 |