题目内容
11.在△ABC内任取一点P (如图①),连接PB、PC,探索∠BPC与∠A,∠ABP,∠ACP之间的数量关系,并证明你的结论:当点P在△ABC外部时 (如图②),请直接写出∠BPC与∠A,∠ABP,∠ACP之间的数量关系.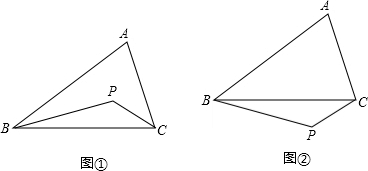
分析 根据三角形的内角和和四边形的内角和即可得到结论.
解答 解:在△ABC内任取一点P,
则∠BPC=∠A+∠ABP+∠ACP,
理由:∵∠BPC=180°-(∠PBC+∠OCB),
∴∠A+∠ABP+∠PBC+∠ACP+∠PCB=180°,
∠A+∠ABP+∠ACP=180°-(∠PBC+∠PCB),
∴∠BPC=∠A+∠ABP+∠ACP;
当点P在△ABC外部时,
∠BPC+∠A+∠ABP+∠ACP=360°.
点评 本题考查了三角形的内角和,四边形的内角和,熟练掌握三角形的内角和是解题的关键.

练习册系列答案
相关题目
16.老师布置了一个探究活动:仅用一架天平和若干个10克的砝码测量1元硬币和5角硬币的质量.(注:同种面值的每枚硬币质量相同).小海同学找来了足够多的1元硬币和5角硬币,经过实验探究,得到了如下的两个探究记录:
请你用所学的数学知识计算出一枚1元硬币多少克,一枚5角硬币多少克?
| 记录 | 天平左边 | 天平右边 | 天平状态 |
| 记录一 | 2枚1元硬币和7枚5角硬币 | 4个10克砝码 | 平衡 |
| 记录二 | 15枚1元硬币 | 20枚5角硬币和1个10克砝码 | 平衡 |
 一次函数经过点A(-2,-1),B(1,3)两点,该函数表示的直线交x轴于点C交y轴于点D
一次函数经过点A(-2,-1),B(1,3)两点,该函数表示的直线交x轴于点C交y轴于点D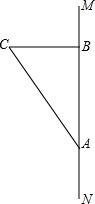 如图所示线段中,A、B为南北方向高速公路MN的两个出站口,A、B相距40km.风景区C在B的正西方向,司机小王由南向北到A后下高速路,沿老路AC到风景区C观光旅游后,再沿C到B后发现从A→C→B共走了50km,但小王不知道从C到B有多少公里,你能用数学知识帮他解决这个问题吗?请你写出求解过程.
如图所示线段中,A、B为南北方向高速公路MN的两个出站口,A、B相距40km.风景区C在B的正西方向,司机小王由南向北到A后下高速路,沿老路AC到风景区C观光旅游后,再沿C到B后发现从A→C→B共走了50km,但小王不知道从C到B有多少公里,你能用数学知识帮他解决这个问题吗?请你写出求解过程.