题目内容
4. 一次函数经过点A(-2,-1),B(1,3)两点,该函数表示的直线交x轴于点C交y轴于点D
一次函数经过点A(-2,-1),B(1,3)两点,该函数表示的直线交x轴于点C交y轴于点D(1)求该一次函数的解析式;
(2)求tan∠OCD的值;
(3)求△AOB的面积.
分析 (1)把A(-2,-1),B(1,3)两点坐标分别代入一次函数y=kx+b,根据待定系数法从而求出其解析式;
(2)根据直线的解析式求得C,D点的坐标,即可得到OD,OC的长,然后接直角三角形即可求得;
(3)根据S△AOB=S△AOC+S△BOC求得即可.
解答 解:(1)设一次函数y=kx+b,
∵一次函数经过点A(-2,-1),B(1,3)两点∴$\left\{\begin{array}{l}{-2k+b=-1}\\{k+b=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=\frac{5}{3}}\end{array}\right.$,
∴该一次函数的解析式为y=$\frac{4}{3}$x+$\frac{5}{3}$;
(2)令y=0,则$\frac{4}{3}$x+$\frac{5}{3}$=0,解得x=-$\frac{5}{4}$,
令x=0,则y=$\frac{5}{3}$,
∴C(-$\frac{5}{4}$,0),D(0,$\frac{5}{3}$).
在Rt△OCD中,OD=$\frac{5}{3}$,OC=$\frac{5}{4}$,
∴tan∠OCD=$\frac{OD}{OC}$=$\frac{4}{3}$;
(3)S△AOB=S△AOC+S△BOC=$\frac{1}{2}$×$\frac{5}{4}$×1+$\frac{1}{2}$×$\frac{5}{4}$×3=$\frac{5}{2}$.
点评 本题考查了待定系数法求一次函数的解析式,一次函数图象上点的坐标特征,锐角三角函数以及三角形面积等,求得C、D的坐标是解题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
19.方程x2-7=0的根是( )
| A. | x=7 | B. | x1=7,x2=-7 | C. | x=$\sqrt{7}$ | D. | x1=-$\sqrt{7}$,x2=$\sqrt{7}$ |
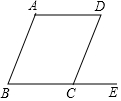 如图,已知AB∥CD,∠B=∠D,AD与BE平行吗?请说明理由.
如图,已知AB∥CD,∠B=∠D,AD与BE平行吗?请说明理由.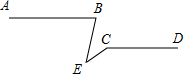 如图,AB∥CD,请探索∠B,∠C,∠E的关系?
如图,AB∥CD,请探索∠B,∠C,∠E的关系?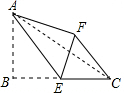 如图,在△ABC中,∠B=90°,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在点F处,连CF,求CF的长.
如图,在△ABC中,∠B=90°,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在点F处,连CF,求CF的长.