题目内容
15.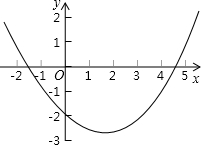 二次函数y=$\frac{1}{3}$x2-x-2的图象如图所示,那么关于x的方程$\frac{1}{3}$x2-x-2=0的近似解为x1=-1.3,x2=4.3(精确到0.1).
二次函数y=$\frac{1}{3}$x2-x-2的图象如图所示,那么关于x的方程$\frac{1}{3}$x2-x-2=0的近似解为x1=-1.3,x2=4.3(精确到0.1).
分析 根据二次函数图象与x轴交点的横坐标是相应的一元二次方程的解,可得一元二次方程的近似根.
解答 解:∵抛物线y=$\frac{1}{3}$x2-x-2与x轴的两个交点分别是(-1.3,0)、(4.3,0),
又∵抛物线y=$\frac{1}{3}$x2-x-2与x轴的两个交点,就是方程$\frac{1}{3}$x2-x-2=0的两个根,
∴方程$\frac{1}{3}$x2-x-2=0的两个近似根是4.3或-1.3
故答案为x1=-1.3,x2=4.3.
点评 本题考查了图象法求一元二次方程的近似根,二次函数图象与x轴交点的横坐标是相应的一元二次方程的解.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
20.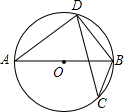 如图,⊙O中,AB是直径,CD是弦,若∠ABD=55°,则∠C等于( )
如图,⊙O中,AB是直径,CD是弦,若∠ABD=55°,则∠C等于( )
 如图,⊙O中,AB是直径,CD是弦,若∠ABD=55°,则∠C等于( )
如图,⊙O中,AB是直径,CD是弦,若∠ABD=55°,则∠C等于( )| A. | 25° | B. | 35° | C. | 45° | D. | 55° |

 如图,在?ABCD中,EF过角线的交点O,若AD=8cm,AB=6cm,OE=4cm,求四边形ABFE的周长.
如图,在?ABCD中,EF过角线的交点O,若AD=8cm,AB=6cm,OE=4cm,求四边形ABFE的周长.