题目内容
5. 如图,在?ABCD中,EF过角线的交点O,若AD=8cm,AB=6cm,OE=4cm,求四边形ABFE的周长.
如图,在?ABCD中,EF过角线的交点O,若AD=8cm,AB=6cm,OE=4cm,求四边形ABFE的周长.
分析 先证明△AOE≌△COF,得出AE=CF,OE=OF=4,EF=8,即可得出四边形ABFE的周长=EF+AE+BF+AB=EF+AB+BC求出答案即可.
解答 解:∵四边形ABCD是平行四边形,
∴CD=AB=6,AD∥BC,OA=OC,
∴∠EAO=∠OCF,
在△AOE和△COF中,$\left\{\begin{array}{l}{∠EAO=∠OCF}&{\;}\\{AO=CO}&{\;}\\{∠AOE=∠COF}&{\;}\end{array}\right.$,
∴△AOE≌△COF(ASA),
∴AE=CF,OE=OF=4,
∴EF=8,
∴四边形ABFE的周长=EF+AE+BF+AB=EF+AB+BC=6+8+8=22(cm).
点评 本题考查了平行四边形的性质、全等三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等得出对应边相等是解决问题的关键.

练习册系列答案
相关题目
10.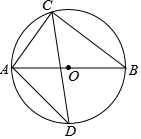 如图,⊙O的直径为AB,弦AC长为6,BC长为8,∠ACB的平分线交⊙O于D,则弦AD的长为( )
如图,⊙O的直径为AB,弦AC长为6,BC长为8,∠ACB的平分线交⊙O于D,则弦AD的长为( )
 如图,⊙O的直径为AB,弦AC长为6,BC长为8,∠ACB的平分线交⊙O于D,则弦AD的长为( )
如图,⊙O的直径为AB,弦AC长为6,BC长为8,∠ACB的平分线交⊙O于D,则弦AD的长为( )| A. | 5$\sqrt{2}$ | B. | 7 | C. | 8$\sqrt{2}$ | D. | 9 |
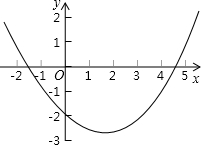 二次函数y=$\frac{1}{3}$x2-x-2的图象如图所示,那么关于x的方程$\frac{1}{3}$x2-x-2=0的近似解为x1=-1.3,x2=4.3(精确到0.1).
二次函数y=$\frac{1}{3}$x2-x-2的图象如图所示,那么关于x的方程$\frac{1}{3}$x2-x-2=0的近似解为x1=-1.3,x2=4.3(精确到0.1).
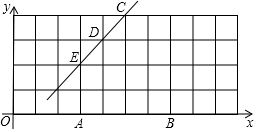 足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好,己知在正方形网格中(每个正方形单位长度都为1),点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,如图建立直角坐标系,则:
足球射门,不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好,己知在正方形网格中(每个正方形单位长度都为1),点A,B,C,D,E均在格点上,球员带球沿CD方向进攻,如图建立直角坐标系,则: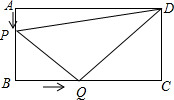 如图所示,在长方形ABCD中,AB=6厘米,BC=12厘米,点P沿AB边从点A开始向点B以1厘米/秒的速度移动,点Q沿BC从点B开始向点C以2厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).
如图所示,在长方形ABCD中,AB=6厘米,BC=12厘米,点P沿AB边从点A开始向点B以1厘米/秒的速度移动,点Q沿BC从点B开始向点C以2厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).