题目内容
6.△ABC中,∠ACB=90°,∠A、∠B、∠C所对的边分别为a、b、c,已知它的周长为6+$\sqrt{26}$且c=$\sqrt{26}$.(1)比较大小6>$\sqrt{26}$;(2)△ABC的面积等于2.5.
分析 (1)直接利用6=$\sqrt{36}$,进而利用实数比较大小方法得出答案;
(2)首先结合勾股定理得出a2+b2=c2=26,进而利用完全平方公式求出答案.
解答 解:(1)∵6=$\sqrt{36}$,
∴6>$\sqrt{26}$;
(2)∵∠ACB=90°,∠A、∠B、∠C所对的边分别为a、b、c,
它的周长为6+$\sqrt{26}$且c=$\sqrt{26}$,
∴a+b=6,a2+b2=c2=26,
∴(a+b)2=36,
∴a2+b2+2ab=36,
∴2ab=10,
∴$\frac{1}{2}$ab=2.5.
故答案为:>,2.5.
点评 此题主要考查了二次根式的应用以及实数比较大小,正确应用完全平方公式是解题关键.

练习册系列答案
相关题目

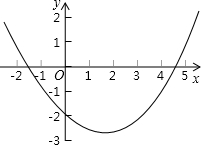 二次函数y=$\frac{1}{3}$x2-x-2的图象如图所示,那么关于x的方程$\frac{1}{3}$x2-x-2=0的近似解为x1=-1.3,x2=4.3(精确到0.1).
二次函数y=$\frac{1}{3}$x2-x-2的图象如图所示,那么关于x的方程$\frac{1}{3}$x2-x-2=0的近似解为x1=-1.3,x2=4.3(精确到0.1).