题目内容
1.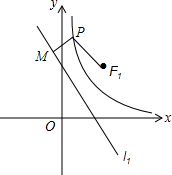 已知直线l1:y=-x$+\sqrt{2}$k,双曲线C:y=$\frac{{k}^{2}}{{x}^{2}}$,定点F1($\sqrt{2}$k,$\sqrt{2}$k).
已知直线l1:y=-x$+\sqrt{2}$k,双曲线C:y=$\frac{{k}^{2}}{{x}^{2}}$,定点F1($\sqrt{2}$k,$\sqrt{2}$k).(1)若k=$\sqrt{2}$,求直线l1,双曲线C的解析式,定点F的坐标;
(2)在(1)的条件下,在双曲线C上任取一点P(x,y),过P作直线l1的垂线段PM,求$\frac{P{F}_{1}}{PM}$的值;
(3)若k为大于0的任意实数,在双曲线C上任取一点P(x,y),过P作直线l1的垂线段PM,判断$\frac{P{F}_{1}}{PM}$的值是否为定值?若是,求出定值;若不是说明理由.
分析 (1)只需把k=$\sqrt{2}$代入直线、双曲线的解析式和点F1的坐标,就可解决问题;
(2)易证△AOB是等腰直角三角形,过点P作PQ∥AB交x轴于点Q,过点Q作QN⊥AB于N,如图,根据平行线间的距离处处相等可得PM=QN.可设PQ的解析式为y=-x+n,设点P的横坐标为a,由此可求出点Q的坐标及AQ的长(用a的代数式表示),在Rt△ANQ中运用三角函数可求出QN(即PM)(用a的代数式表示),然后运用两点之间距离公式可求出PF1(用a的代数式表示),就可求出$\frac{P{F}_{1}}{PM}$的值;
(3)易证△AOB是等腰直角三角形,过点P作PQ∥AB交x轴于点Q,过点Q作QN⊥AB于N,如图,根据平行线间的距离处处相等可得PM=QN.可设PQ的解析式为y=-x+n,设点P的横坐标为a,由此可求出点Q的坐标及AQ的长(用a和k的代数式表示),在Rt△ANQ中运用三角函数可求出QN(即PM)(用a和k的代数式表示),然后运用两点之间距离公式可求出PF1(用a和k的代数式表示),就可求出$\frac{P{F}_{1}}{PM}$的值.
解答 解:(1)当若k=$\sqrt{2}$时,
直线l1的解析式为y=-x+2,双曲线C的解析式为y=$\frac{2}{x}$,定点F1的坐标为(2,2);
(2)∵A、B分别是直线y=-x+2与x轴、y轴的交点,
∴A(2,0)、B(0,2),
∴OA=OB=2.
∵∠AOB=90°,
∴∠OAB=∠OBA=45°.
过点P作PQ∥AB交x轴于点Q,过点Q作QN⊥AB于N,如图所示,
则有PM=QN.
可设PQ的解析式为y=-x+n.
设点P的横坐标为a,则yP=$\frac{2}{a}$,
∴$\frac{2}{a}$=-a+n,
∴n=$\frac{2}{a}$+a,
∴直线PQ的解析式为y=-x+$\frac{2}{a}$+a.
当y=0时,-x+$\frac{2}{a}$+a=0,
∴x=$\frac{2}{a}$+a,
∴Q($\frac{2}{a}$+a,0),OQ=$\frac{2}{a}$+a,
∴AQ=$\frac{2}{a}$+a-2,
∴PM=QN=AQ•sin∠QAN=$\frac{\sqrt{2}}{2}$($\frac{2}{a}$+a-2).
∵P(a,$\frac{2}{a}$),F1(2,2),
∴PF1=$\sqrt{(a-2)^{2}+(\frac{2}{a}-2)^{2}}$
=$\sqrt{{a}^{2}-4a+4+\frac{4}{{a}^{2}}-\frac{8}{a}+4}$
=$\sqrt{(a+\frac{2}{a})^{2}-4(a+\frac{2}{a})+4}$
=$\sqrt{(a+\frac{2}{a}-2)^{2}}$
=$\frac{2}{a}$+a-2.
∴PM=$\frac{\sqrt{2}}{2}$PF1,
∴$\frac{P{F}_{1}}{PM}$=$\sqrt{2}$;
(3)$\frac{P{F}_{1}}{PM}$的值是定值.
∵A、B分别是直线y=-x+$\sqrt{2}$k与x轴、y轴的交点,
∴A($\sqrt{2}$k,0)、B(0,$\sqrt{2}$k),
∴OA=OB=$\sqrt{2}$k.
∵∠AOB=90°,
∴∠OAB=∠OBA=45°.
过点P作PQ∥AB交x轴于点Q,过点Q作QN⊥AB于N,如图所示,
则有PM=QN.
可设PQ的解析式为y=-x+n.
设点P的横坐标为a,则yP=$\frac{{k}^{2}}{a}$,
∴$\frac{{k}^{2}}{a}$=-a+n,
∴n=$\frac{{k}^{2}}{a}$+a,
∴直线PQ的解析式为y=-x+$\frac{{k}^{2}}{a}$+a,
当y=0时,-x+$\frac{{k}^{2}}{a}$+a=0,
∴x=$\frac{{k}^{2}}{a}$+a,
∴Q($\frac{{k}^{2}}{a}$+a,0),OQ=$\frac{{k}^{2}}{a}$+a,
∴AQ=$\frac{{k}^{2}}{a}$+a-$\sqrt{2}$k,
∴PM=QN=AQ•sin∠QAN=$\frac{\sqrt{2}}{2}$($\frac{{k}^{2}}{a}$+a-$\sqrt{2}$k).
∵P(a,$\frac{{k}^{2}}{a}$),F1($\sqrt{2}$k,$\sqrt{2}$k),
∴PF1=$\sqrt{(a-\sqrt{2}k)^{2}+(\frac{{k}^{2}}{a}-\sqrt{2}k)^{2}}$
=$\sqrt{{a}^{2}+\frac{{k}^{4}}{{a}^{2}}-2\sqrt{2}k(a+\frac{{k}^{2}}{a})+4{k}^{2}}$
=$\sqrt{(a+\frac{{k}^{2}}{a}-\sqrt{2}k)^{2}}$
=a+$\frac{{k}^{2}}{a}$-$\sqrt{2}$k,
∴PM=$\frac{\sqrt{2}}{2}$PF1,
∴$\frac{P{F}_{1}}{PM}$=$\sqrt{2}$.
点评 本题主要考查了直线及反比例函数图象上点的坐标特征、运用待定系数法求直线的解析式、两直线平行的问题、平行线间的距离处处相等、三角函数、两点之间的距离公式等知识,利用平行线间的距离处处相等将PM转化为QN,是解决本题的关键;运用两点之间距离公式时,将根号内的代数式配成完全平方是解决本题的难点.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案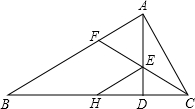 如图,∠BAC=90°,AD⊥BC于D,∠ACB的平分线交AD于E,交AB于F,过E作EH∥AB,交BC于H,求证:AF=EH.
如图,∠BAC=90°,AD⊥BC于D,∠ACB的平分线交AD于E,交AB于F,过E作EH∥AB,交BC于H,求证:AF=EH.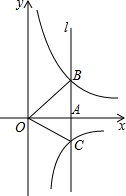 如图,经过点A(3,0)的直线l平行于y轴,与双曲线y=$\frac{4}{x}$和y=$\frac{k}{x}$分别交于点B和C.
如图,经过点A(3,0)的直线l平行于y轴,与双曲线y=$\frac{4}{x}$和y=$\frac{k}{x}$分别交于点B和C.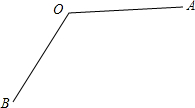 (1)用尺规作图的方法,作出∠AOB的平分线OC(保留作图痕迹,不要求写出作法);
(1)用尺规作图的方法,作出∠AOB的平分线OC(保留作图痕迹,不要求写出作法);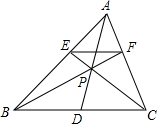 如图,△ABC中,E、F在AB、AC上,EF∥BC,BF、CE交于点P,延长AP交BC于点D,求证:BD=CD.
如图,△ABC中,E、F在AB、AC上,EF∥BC,BF、CE交于点P,延长AP交BC于点D,求证:BD=CD.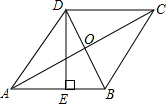 如图,在菱形ABCD中,DE=AO,DE⊥AB,AB=2.
如图,在菱形ABCD中,DE=AO,DE⊥AB,AB=2.