题目内容
16.如果A=$\root{a-2b+3}{a+3b}$是a+3b的算术平方根,B=$\root{2a-b-1}{1-{a}^{2}}$的1-a2的立方根.试求:A-B的平方根.
分析 根据算术平方根与立方根的定义得到$\left\{\begin{array}{l}{a-2b+3=2}\\{2a-b-1=3}\end{array}\right.$,解方程组可计算出a,b,然后计算A-B后利用平方根的定义求解.
解答 解:依题意有$\left\{\begin{array}{l}{a-2b+3=2}\\{2a-b-1=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=3}\\{b=2}\end{array}\right.$,
A=$\sqrt{9}$=3,
B=$\root{3}{-8}$=-2
A-B=3+2=5,
故A-B的平方根是±$\sqrt{5}$.
点评 本题考查了立方根:如果一个数的立方等于a,那么这个数叫做a的立方根或三次方根.这就是说,如果x3=a,那么x叫做a的立方根.记作:$\root{3}{a}$.也考查了平方根与算术平方根.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
6.如果将长为8cm,宽为6cm的矩形纸片折叠一次,那么这条折痕的长不可能是( )
| A. | 7cm | B. | 8cm | C. | 10cm | D. | 11cm |
4.从一块半径是4m的圆形铁片上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是( )
| A. | $\sqrt{2}$m | B. | 2m | C. | 4m | D. | $\sqrt{15}$m |
1. 右图是某几何体的三视图,这个几何体是( )
右图是某几何体的三视图,这个几何体是( )
 右图是某几何体的三视图,这个几何体是( )
右图是某几何体的三视图,这个几何体是( )| A. | 圆柱 | B. | 三棱柱 | C. | 球 | D. | 圆锥 |
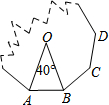 如图,一个正n边形纸片被撕掉了一部分,已知它的中心角是40°,那么n=9.
如图,一个正n边形纸片被撕掉了一部分,已知它的中心角是40°,那么n=9.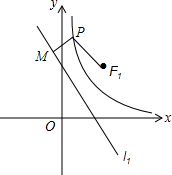 已知直线l1:y=-x$+\sqrt{2}$k,双曲线C:y=$\frac{{k}^{2}}{{x}^{2}}$,定点F1($\sqrt{2}$k,$\sqrt{2}$k).
已知直线l1:y=-x$+\sqrt{2}$k,双曲线C:y=$\frac{{k}^{2}}{{x}^{2}}$,定点F1($\sqrt{2}$k,$\sqrt{2}$k).