题目内容
11.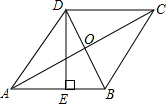 如图,在菱形ABCD中,DE=AO,DE⊥AB,AB=2.
如图,在菱形ABCD中,DE=AO,DE⊥AB,AB=2.(1)求∠ABC的度数;
(2)求菱形ABCD的面积.
分析 (1)直接利用菱形的性质结合三角形面积求法,得出△ABD是等边三角形,即可得出答案;
(2)直接利用(1)中所求得出AO的长,进而求出菱形面积.
解答 解:(1)∵四边形ABCD是菱形,
∴BD⊥AC,AD=AB,
∵DE=AO,DE⊥AB,
∴DE×AB=AO×BD,
∴AB=BD,
∴AD=AB=BD,
∴△ABD是等边三角形,
∴∠DAB=60°,
∴∠ABC=120°;
(2)∵AB=2,∠DAB=60°,
∴∠DAO=30°,BD=2,
∴AO=$\sqrt{3}$,
∴AC=2$\sqrt{3}$,
∴菱形ABCD的面积为:$\frac{1}{2}$×2×2$\sqrt{3}$=2$\sqrt{3}$.
点评 此题主要考查了菱形的性质以及等边三角形的判定与性质,正确应用菱形的性质是解题关键.

练习册系列答案
相关题目
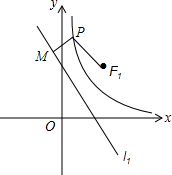 已知直线l1:y=-x$+\sqrt{2}$k,双曲线C:y=$\frac{{k}^{2}}{{x}^{2}}$,定点F1($\sqrt{2}$k,$\sqrt{2}$k).
已知直线l1:y=-x$+\sqrt{2}$k,双曲线C:y=$\frac{{k}^{2}}{{x}^{2}}$,定点F1($\sqrt{2}$k,$\sqrt{2}$k).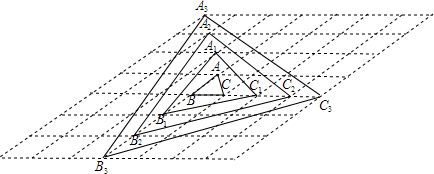
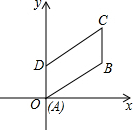 如图,在平行四边形ABCD中,∠DAB=60°,AB=2,AD=1,若点A在坐标原点,AB与x轴的夹角为30°,求平行四边形各顶点的坐标.
如图,在平行四边形ABCD中,∠DAB=60°,AB=2,AD=1,若点A在坐标原点,AB与x轴的夹角为30°,求平行四边形各顶点的坐标.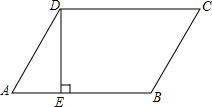 如图,在平行四边形ABCD中,AD=BC,AB=CD,DE⊥AB于点E,∠A=60°,BE=2AE=$\sqrt{72}$cm,求平行四边形ABCD的周长.
如图,在平行四边形ABCD中,AD=BC,AB=CD,DE⊥AB于点E,∠A=60°,BE=2AE=$\sqrt{72}$cm,求平行四边形ABCD的周长.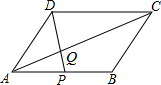 如图,在?ABCD中,点P在AB上,连结DP,交AC于点Q,当点P是AB的中点时,△ADQ的面积为1,则?ABCD的面积为( )
如图,在?ABCD中,点P在AB上,连结DP,交AC于点Q,当点P是AB的中点时,△ADQ的面积为1,则?ABCD的面积为( )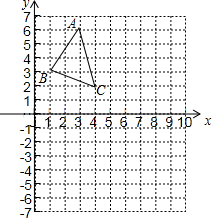 如图,△ABC的顶点坐标分别是A(3,6)、B(1,3)、C(4,2).
如图,△ABC的顶点坐标分别是A(3,6)、B(1,3)、C(4,2).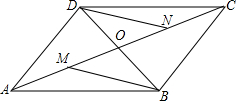 如图所示,?ABCD的对角线AC,BD相交于O,M是AO的中点,N是CO的中点,则BM与DN有什么关系?证明你的结论.
如图所示,?ABCD的对角线AC,BD相交于O,M是AO的中点,N是CO的中点,则BM与DN有什么关系?证明你的结论.