题目内容
9.已知平行四边形的周长为12,一边长为x,且这边上的高为(x+2),设平行四边形的面积为S.(1)请写出S关于x的函数表达式,并写出自变量x的取值范围;
(2)当平行四边形为矩形时,求S的值.
分析 (1)根据面积公式,可得函数解析式;根据周长公式,可得另一边的长,根据边长是正数,斜边长大于直角边的长,可得自变量的取值范围;
(2)根据矩形的面积公式,可得答案.
解答 解:(1)由平行四边形的面积公式,得
S=x(x+2).
由平行四边形的周长公式,得
另一边的长是(6-x),
由边长是正数,斜边长大于直角边的长,得
x>0,且6-x>x+2.
解得0<x<4;
S=x(x+2),自变量的取值范围0<x<4;
(2)由矩形的面积公式,得
S=x(6-x),自变量的取值范围0<x<6.
点评 本题考查了函数关系式,利用平行四边形的面积公式是解题关键.

练习册系列答案
相关题目
4.从一块半径是4m的圆形铁片上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是( )
| A. | $\sqrt{2}$m | B. | 2m | C. | 4m | D. | $\sqrt{15}$m |
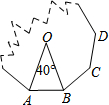 如图,一个正n边形纸片被撕掉了一部分,已知它的中心角是40°,那么n=9.
如图,一个正n边形纸片被撕掉了一部分,已知它的中心角是40°,那么n=9.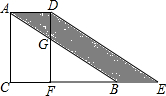 将直角三角形ABC沿CB方向平移CF的长度后,得到直角三角形DEF.已知DG=4,CF=6,AC=10,求阴影部分的面积.
将直角三角形ABC沿CB方向平移CF的长度后,得到直角三角形DEF.已知DG=4,CF=6,AC=10,求阴影部分的面积. 如图,AC∥CD,AP和CP分别平分∠BAC和∠ACD,过点P分别作PG⊥AC于点G,PE⊥AB于点E,EP的延长线交CD于点F.
如图,AC∥CD,AP和CP分别平分∠BAC和∠ACD,过点P分别作PG⊥AC于点G,PE⊥AB于点E,EP的延长线交CD于点F.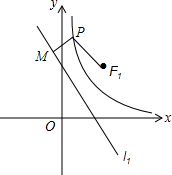 已知直线l1:y=-x$+\sqrt{2}$k,双曲线C:y=$\frac{{k}^{2}}{{x}^{2}}$,定点F1($\sqrt{2}$k,$\sqrt{2}$k).
已知直线l1:y=-x$+\sqrt{2}$k,双曲线C:y=$\frac{{k}^{2}}{{x}^{2}}$,定点F1($\sqrt{2}$k,$\sqrt{2}$k).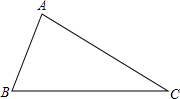 已知如图,在△ABC中,∠B=2∠C.
已知如图,在△ABC中,∠B=2∠C.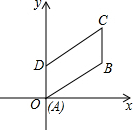 如图,在平行四边形ABCD中,∠DAB=60°,AB=2,AD=1,若点A在坐标原点,AB与x轴的夹角为30°,求平行四边形各顶点的坐标.
如图,在平行四边形ABCD中,∠DAB=60°,AB=2,AD=1,若点A在坐标原点,AB与x轴的夹角为30°,求平行四边形各顶点的坐标.