题目内容
10．
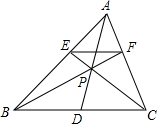如图，△ABC中，E、F在AB、AC上，EF∥BC，BF、CE交于点P，延长AP交BC于点D，求证：BD=CD．
分析 根据相似三角形的性质可得$\frac{EG}{BD}$=$\frac{AE}{AB}$=$\frac{EF}{BC}$=$\frac{EP}{PC}$=$\frac{EG}{DC}$，即可得到BD=DC．
解答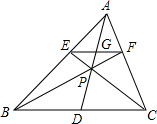 
证明：∵EF∥BC，
∴△AEG∽△ABD，
∴$\frac{EG}{BD}$=$\frac{AE}{AB}$．
同理可得：
$\frac{AE}{AB}$=$\frac{EF}{BC}$，$\frac{EF}{BC}$=$\frac{EP}{PC}$，$\frac{EP}{PC}$=$\frac{EG}{DC}$，
∴$\frac{EG}{BD}$=$\frac{EG}{DC}$，
∴BD=DC．
点评 本题主要考查的是相似三角形的判定与性质，从中可提炼出一个重要的结论：若EF∥BC，则直线AP平分BC．
练习册系列答案
相关题目
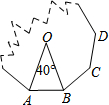如图，一个正n边形纸片被撕掉了一部分，已知它的中心角是40°，那么n=9．
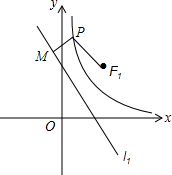已知直线l1：y=-x$+\sqrt{2}$k，双曲线C：y=$\frac{{k}^{2}}{{x}^{2}}$，定点F1（$\sqrt{2}$k，$\sqrt{2}$k）．
已知如图，在△ABC中，∠B=2∠C．
5．菱形中某两个角的和是90°，周长是12，则菱形的面积是（ ）
| A． | $\frac{3\sqrt{2}}{2}$ | B． | $\frac{5\sqrt{2}}{2}$ | C． | $\frac{7\sqrt{2}}{2}$ | D． | $\frac{9\sqrt{2}}{2}$ |
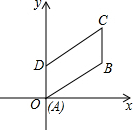如图，在平行四边形ABCD中，∠DAB=60°，AB=2，AD=1，若点A在坐标原点，AB与x轴的夹角为30°，求平行四边形各顶点的坐标．