题目内容
13.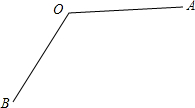 (1)用尺规作图的方法,作出∠AOB的平分线OC(保留作图痕迹,不要求写出作法);
(1)用尺规作图的方法,作出∠AOB的平分线OC(保留作图痕迹,不要求写出作法);(2)在(1)中所作的射线OC上任取一点M,过点M作MN⊥OA于点N,过点M作MP⊥OB于点P.求证:NO=PO.
分析 (1)利用基本作图(作已知角的角平分线)作OC平分∠AOB;
(2)先根据角平分线的性质定理得到MN=MP,然后利用“HL”证明Rt△MON≌Rt△MOP,则根据全等三角形的性质即可得到结论.
解答 (1)解:如图,OC为所作;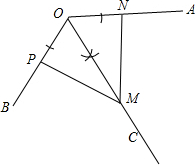
(2)证明:∵OC平分∠AOB,
而MN⊥OA,MP⊥OB,
∴MN=MP,
在Rt△MON和Rt△MOP中,
$\left\{\begin{array}{l}{MO=MO}\\{MN=MP}\end{array}\right.$,
∴Rt△MON≌Rt△MOP,
∴NO=PO.
点评 本题考查了作图-基本作图:作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
5.菱形中某两个角的和是90°,周长是12,则菱形的面积是( )
| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{5\sqrt{2}}{2}$ | C. | $\frac{7\sqrt{2}}{2}$ | D. | $\frac{9\sqrt{2}}{2}$ |
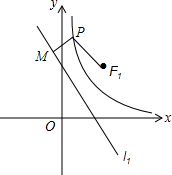 已知直线l1:y=-x$+\sqrt{2}$k,双曲线C:y=$\frac{{k}^{2}}{{x}^{2}}$,定点F1($\sqrt{2}$k,$\sqrt{2}$k).
已知直线l1:y=-x$+\sqrt{2}$k,双曲线C:y=$\frac{{k}^{2}}{{x}^{2}}$,定点F1($\sqrt{2}$k,$\sqrt{2}$k). 已知如图,在△ABC中,∠B=2∠C.
已知如图,在△ABC中,∠B=2∠C.
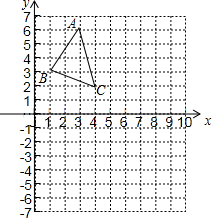 如图,△ABC的顶点坐标分别是A(3,6)、B(1,3)、C(4,2).
如图,△ABC的顶点坐标分别是A(3,6)、B(1,3)、C(4,2).